.
.
Увы, но мне пока не нравится.
Придётся мне сделать небольшой экскурс в устройство звука, музыки и суть моей идеи.
Не буду рассказывать, что любой звуковой сигнал (а в общем случае — вообще любой сиганл, вовсе не обязательно звуковой) можно разложить на составляющие (сумму синусоид) и на основе этого получить спектр сигнала.
Подойдём с другой стороны. Если вы далеки от музыки и/или обработки сигналов, то возможно вы слышали такой термин
октава, и считаете, что это что-то, что музыканты сперва придумали себе, а затем обозвали этим словом. На самом деле, это одна из немногих вещей, которую никто не придумал (в чистом виде), а которая является
мировой данностью.
Как, например, число Пи. Никто не придумывал число Пи в том смысле, что никто не размышлял в стиле «я обдумал много вариантов и выбираю этот». Само по себе число не изобретено кем-либо, а является
общемировой истиной. Его значение не зависит от чьего-либо авторитетного мнения, не меняется с ходом времени. Его значение существовало до возникновения человека, будет существовать после исчезновения человека, и в целом, может существовать без существования самого человека.
Единственное, что сделал человек: это нашёл закономерность между длиной окружности и диаметром, понял, что соотношение всегда одинаково и дал этому числу название. Мог дать другое название. Каждый человек мог дать своё название. Название могло бы быть дано на 1000 лет раньше или позже. Но само число от этого никак не меняется. Оно само и связанная с ним закономерность существует вне зависимости от наличия от названия и того, известна ли кому эта закономерность.
Аналогичным образом дело обстоит с
октавой.
Октава — это превосходство в два раза. Превосходство частоты чего-то, например частоты сигнала. «На октаву выше» означает, что один частота одного сигнала больше частоты другого ровно
в два раза. «На октаву ниже» — значит в два раза меньше.
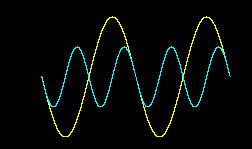 (голубой сигнал на 1 октаву выше желтого)
(голубой сигнал на 1 октаву выше желтого)Люди просто обнаружили особое свойство такого сочетания частот (при таком сочетании частот периоды колебаний оказываются кратными, причём наступление у обоих сигналов одной фазы происходит максимально часто (для соотношения частот 1:2 мы имеем минимальный НОК для периодов колебаний)) и решили такое сочетание частот как-то назвать. И назвали октавой.
На самом деле, история несколько упрощена, и в слове октава мы можете найти латинский корень oct, который означает число 8, но это всё несущественные детали.Итак, октава — это соотношение частот как 1:2. Если одна частота будет в 8 раз больше другой, то она будет выше «на три октавы». Синусоидальный сигнал с частотой 5 герц (который вы даже не услышите, ибо это инфразвук) на семь октав ниже, чем тот же синус 640 Гц. А синусоидальный сигнал с частотой 666 Гц на одну октаву выше, чем синусоидальный сигнал частотой 333 Гц.
По сути, октава — это безразмерная единица для выражения
относительной разницы двух частот. Точно такая же, как
децибел является безразмерной единицей для выражения относительной разницы двух уровней. Единицами для выражения абсолютной разницы были бы, к примеру, герцы и вольты (или ватты, или что-то ещё) соответственно.
Как и в случае с децибелами, здесь всё крутится вокруг логарифмической шкалы: если какие-либо величины отмечать точками на шкале с линейным масштабом, то расстояние между двумя любыми точками будут пропорционально тому
на сколько одна больше другой, в то время, как если те же величины отмечать точками на шкале с логарифмическим масштабом — расстояние между любыми двумя точками будет пропорционально тому,
во сколько раз одна величина больше другой.
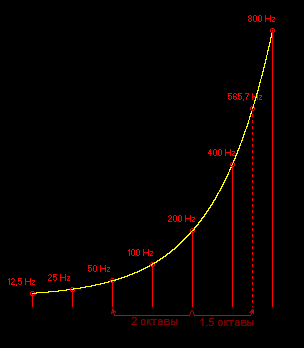
Если f1 на n октав выше, чем f2, значит f1 = f2 × 2nКак вы понимаете, показатель степени не обязательно должен быть целым, поэтому интервал между двумя тонами не обязан измеряться целым числом октав. Синусоидальный сигнал частотой 200 Гц на две октавы выше, чем сигнал 50 Гц, но на 1.5 октавы ниже, чем сигнал 565.7 Гц.
Обратное:
Если два тона имеют частоты f1 и f2, значит интервал между ними в октавах: n = log2(f2) – log2(f1) = log2(f2 / f1)Итак, октава — одна из действительно немногих вещей в музыке, которую люди не сами придумали и привнесли в свою науку, а которую они просто заметили (как закономерность) и дали ей какое-то имя. Из любых двух сочетаний двух одновременно звучащих тонов, большинство сочетаний звучит просто отвратительно, некоторые сочетания дают «интересные» звучания, в которых слышатся два звучащих тона, и лишь два тона, интервал между которыми составляет октава (либо кратен октаве) звучат как один тон, но более «жирный». Если от психо-аккустического восприятия провести аналогию к графическому: такие тона воспринимаются как подобные треугольники, отличающиеся своими размерами, но не формой.
Дальше начинается царство соглашений.
Музыка родилась для человечества раньше многих вещей, раньше письменности, может быть даже раньше речи. Первоначально человечество для звукоизвлечения пользовалось тем, что под рукой, через какое-то время люди начали конструировать инструменты в соответствии со своими требованиями. Отбросим инструменты, которые издают всевозможные шумы, то есть звуки, спектр которых состоит из конкретных «томов», а из огромного множества элементарных составляющих всех возможных частот.
Возьмём самый просто пример: пень с щепкой.
 (кадр из мультфильма «Вершки и корешки»)
(кадр из мультфильма «Вершки и корешки»)Методика извлечения звука из щепки проста: вы, прикладывая усилие, оттягиваете конец щепки на какое-то расстояние и отпускаете его. Под действием силы упругости щепка стремится вернуться в нейтральное положение, но за время своего движения из крайнего положения в нейтральное она успевает приобрести некоторую скоростью и за счёт инерции попросту пролетает нейтральное положение и уходит существенно дальше него, оказываясь на момент погашения скорости в противоположенном крайней положении. Цикл многократно повторяется и останавливается только з асчёт потерь энергии на деформацию и рассеяние её в окружающую среду. Типичный маятник.
У играющего на щепке нет возможности менять тон получаемого звука, а есть только возможность менять амплитуду колебаний (т.е. интенсивность получаемого звука), варьируя величину изначального отклонения щепки от нейтрального положения.
Частота, с которой щепка совершает начинает совершать колебания после отпускания из крайнего положения, зависит от упругости материала щепки, массы щепки (зависящей от геометрии щепки) и в малой степени — от параметров окружающей среды. На самом деле у играющего всё же есть возможность менять длину колеблющейся части щепки и таким образом изменять массу колеблющейся части и, в свою очередь, таким образом менять частоту колебаний и производимый тон, но это технически сложно, поэтому этот аспект мы не рассматриваем.
Частота таких колебаний может быть относительно легко вычислена, и допустим, мы её назовём
f0.
Однако, ключевой факт номер 1 состоит в том, что в силу явления резонанса, в щепке возникают не только колебания с частотой
fr, но и колебания на частотах, кратных
fr.
И получается, что колебания щепки составляют суперпозицию колебаний на частотах
f0, 2
·f0, 3·
f0, 4·
f0, ... k·
f0Синусоидальные колебания на частоте
f0 называются
основным тоном, а колебания на более высоких кратных частотах —
обертонами. Собственно, «обер» — это немецкое «над», точно такое же, как английское
over.
(Существует так же термин, унтертоны — смысл слова, я думаю, понятен по аналогии)Именно наличие обертонов даёт щепке характерное звучание; именно в силу наличия обертонов щепка не звучит как одиночные синусоидальные колебания на определённой частоте.
Теоретически, когда звучит щепка, ряд получаемых обертонов — бесконечен. На практике же абсолютно все колебания (и основной тон и обертоны) затухают, причём для чем выше частота колебаний — тем быстрее они затухают. Поэтому на практике ряд обертонов можно считать ограниченным сверху — слишком высокочастотные обертоны затухают практически мгновенно, по крайней мере, до уровня, при котором ухо (да и другие звукофиксирующие устройства) не могут их зафиксировать, потому что их интенсивность в на много порядков ниже интенсивности того же основного тона.
Спектр звука, издаваемого вибрирующей щепкой в начальный момент её звучания:
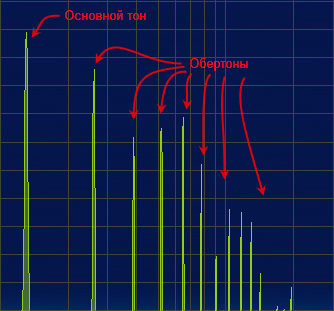
Горизонтальная ось — частоты, вертикальная — интенсивность соответствующих колебаний. Шкала по горизонтали — логарифмическая. Цена горизонтального деления — сначала 100 Гц, затем 1000 Гц.
Вообще, для любых инструментов спектральный состав звука и характер изменения каждой спектральной составляющей по интенсивности (а иногда и частоте) во времени — определяет уникальный тембр этого инструмента.
Это же относится к такому инструменту как человеческий голос. Спектрограмма человеческого голоса:
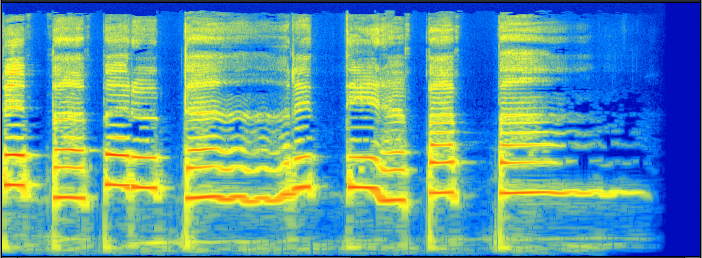
Горизонтальная ось — время, линейный масштаб. Вертикальная ось — частота, логарифмический масштаб.
Всё вышесказанное об основном тоне и обертонах, как видно, в той же степени относится и к голосу, поскольку голосовая щель представляет такую же резонирующую систему, как и щепка на пне, и в целом голосовые складки аналогичны струнам: человек регулирует высоту тона изменяя силу натяжения
струны складок. На спектрограмме видно, что наиболее сильно проявляются основной тон и первый обертон, отстоящие друг от друга на одну октаву.
Итак, если у вас есть пень с щепкой, вы можете сыграть на нём определённый
ритм, но вы не можете сыграть какую-либо мелодию, потому что пень с щепкой всё время издаёт тон одной и той же высоты (частота основного тона, а значит и частоты всех обертонов, все время одни и те же). С учётом того, что человеческий голос позволяет менять высоту тона и издавать любые тона из некоторого диапазона, понятно, что человеку хотелось иметь инструмент, способный издавать более чем одну ноту. Поэтому такие инструменты были созданы.
Не важно, каким интерфейсом обладает интерфейс: клавиши ли, или струны, или площадки, по которому нужно ударять молоточком, или трубки, в которые нужно дуть — из набора звуков произвольных частот музыка как-то не получалась, поэтому стала понятна необходимость наличия дискретного набора звуков определённой высоты — нот.
Особая взаимосвязь ряда звуков, отстоящих друг от друга по высоте (по частоте) на интервал в одну октаву, была известен давно, однако же если в качестве нот использовать этот ряд звуков, то ничего интересного из этого не получится: интервал в одну октаву слишком велик, но что ещё хуже, все ноты, тон которых отстоит друг от друга на одну октаву, обладают очень хорошо ощущаемым звуковым сродством и воспринимаются как «одна и та же по сути» нота но с разной высотой звучания. Причём, чем богаче обертоновый состав таких нот (и чем меньшей и более гладкой разница между интенсивностью обертонов), тем менее выраженной становится разница между такими нотами.
Поэтому взять в качестве нот звуки, расположенные по сетке частот с шагом в октаву — не подходит. Конечно, какую-то музыку с большой натяжкой на такое звание и можно было бы сочинить и исполнить, но...
Естественно возникающая мысль: разбить октавную сетку на более мелкие интервалы и взять промежуточные точки в качестве нот. С учётом того, что человечество легко установило связь тона и длину/натяжённости струны, это не было большой проблемой, и меняя какой-либо параметр (длину/натяжённость) можно было получать тон произвольной высоты.
Однако тут возникают
три главных вопроса, которые лежат в основе необходимости ввода конвенций:
- На сколько более мелких интервалов делить октаву? Два? Три? Пять? Десять? Двадцать?
- По какому принципу делить октаву? Должны ли интервалы быть равными? Должны ли они быть равными в абсолютном или относительном выражении?
- От какой частоты строить октавную сетку?
По сути, если представить, что нам известен только тот факт, что интервал в октаву обладает уникальными свойствами (в первую очередь с точки зрения восприятия) и что он соответствует превосходству частоты вдвое, у нас есть только следующая картина:
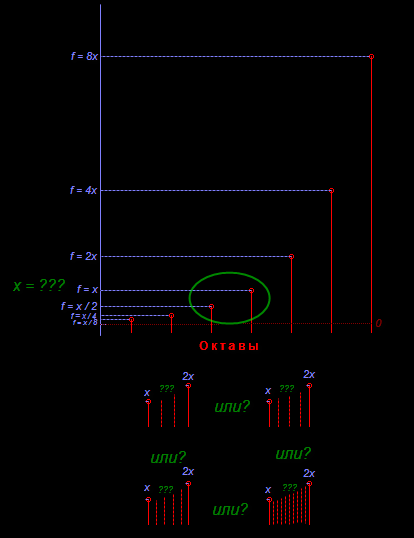
Непонятно, чему должен быть равен
x, на сколько кусочков делить октаву чтобы получить промежуточные ноты и, что ещё важнее, даже если будет определено это число, как вычислить частоту конкретной промежуточной точки (и в соответствие ей подобрать длину или силу натяжения струны, к примеру)?
Попытки решить эту проблему предпринимались очень давно, как минимум ещё до нашей эры, в результате чего был принят
Пифагоров строй.
Вообще,
строй — это и есть концепция того или соглашение о том, как и на какое количество интервалов делить октаву, чтобы получить «промежуточные» ноты. Поскольку такие вещи, как показательная функция и логарифм не были известны людям в древности, попытки поделить октаву предпринимались на основе дробления её на такие интервалы, что соотношения между частотами соседних нот описывалось бы соотношением натуральных чисел.
Строев было создано несколько:
Причина, по которой были созданы разные строи, в том, что ни один из вариантов решения проблемы не был абсолютно идеальным. Попытки разделить октаву на промежуточные ноты, используя подход, при котором частоты нот вычислялись через соотношения натуральных чисел, давали такую сетку частот, что некоторые интервалы звучали откровенно плохо (т.н. «фальшиво»).
Так, например, с некоторым упрощением изложения, можно сказать, что натуральный строй предполагал разделение октавы на 12 примерно равных (на слух) интервалов с образованием таким образом в каждой октаве 12 нот.
Интервалы между соседними нотами не были абсолютно идентичными: пропорция частот между двумя соседними нотами могла быть либо 15:16, либо 128:135, либо 24:25.
Тем не менее, благодаря развитию математики и постоянному поиску идеального строя, сначала был предложен и математическим образом рассчитан, а потом (начиная с 18-го века) и получил роль господствующего строй, который можно считать математически идеальным и который используется по сегодняшний день —
равномерно темперированный строй.
Идея проста:
- октава делится на 12 истинно равных кусочков (интервалов), с получением в каждой октаве 12 нот.
- Поскольку октава — это соотношение частот 1:2, а мы делим её на 12 интервалов, каждый интервал — это соотношение частот 1:21/12
- частота каждой последующей ноты больше частоты предыдущей ноты в 21/12 раза
Кроме того, как и на сколько промежуточных нот разделить октаву, на вопрос о том, какую частоту брать в качестве опорной, чтобы на её основе расчитывать частоты всех остальных нот, тоже был дан ответ. Хотя это число не подкреплено никакой абсолютной истиной и ничем не лучше и не хуже других чисел, за опорную частоту была принята частота в 440 Гц, хотя в разное время в качестве опорной частоты принимались хоть и близкие, но отличающиеся частоты. До сегодняшнего дня существуют и отдельные музыканты и оркестры, которые свои инструменты настраивают используя в качестве опорной частоты
Тут стоит заметить, что вся суть равномерно темперированного строя не в делении октавы именно на 12 интервалов, а в делении её именно на математически равные (соотношения частот между любыми двумя соседними нотами одинаково для любой пары соседних нот). 12-ступенчатое деление — это всего лишь частный случай (хоть и имеющий абсолютно превосходящее по сравнению с другими распространение). Существуют произведения, написанные для равномерной темперации, при которой октава делится, к примеру, на 24 интервала, а не на 12.
Этот интервал в одну двенадцатую октавы называется полутоном, а две таких интервала образуют целый тон. Таким образом, получается, октава как интервал состоит из 12 полутонов или 6 тонов.
(Вообще-то полутона — понятие актуально и для других строев, для того же натурального строя, только в нём есть целых три типа немного отличающихся друг от друга полутонов).Т.е. и «октава» и «полутон» являются единицами измерения и в принципе обладают одной и той же размерностью (безразмерны как и децибел).
Вообще, названия «тонов» и «полутонов», латинское «восемь» (oct) в корне слова «октава» и традиция наличия и определённого способа комбинирования на клавиатурах клавишных инструментах черных и белых клавиш восходят к периодам, когда использовались неравномерно темперированные строи, в связи с чем интервал между соседней белой и соседней чёрной клавишами был был отличен от поделенного на два интервала между двумя белыми клавишами. С введением равномерно темперированного смысла по крайней мере деление клавиш на чёрные и белые потеряло всякий смысл (кроме удобства и исторически сложившейся традиции), поскольку все клавиши равнозначны и интервалы между частотами любых двух соседних клавиш — идентичны.
Поэтому:
- То, что октава это соотношение частот 1:2 — это мировая истина. Истина такого же порядка, как число Пи.
- Деление октавы именно на 12 ступеней, использование равных ступеней и выбор частоты 440 Гц — это предмет соглашения между людьми. Есть другие соглашения. Они вряд ли менее правильные и вряд ли более правильные. Просто одни соглашения более популярны, а другие — менее популярны.
Получается, в современной музыке используется следующее сопоставление нот и частот их базового тона:
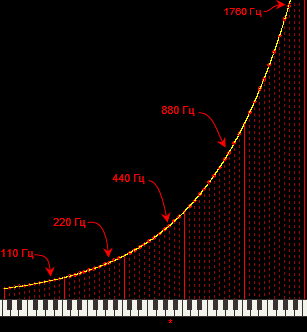
А если вам интересно, насколько отличаются частоты соответствующих нот натурального и равномерного темперированного строев:
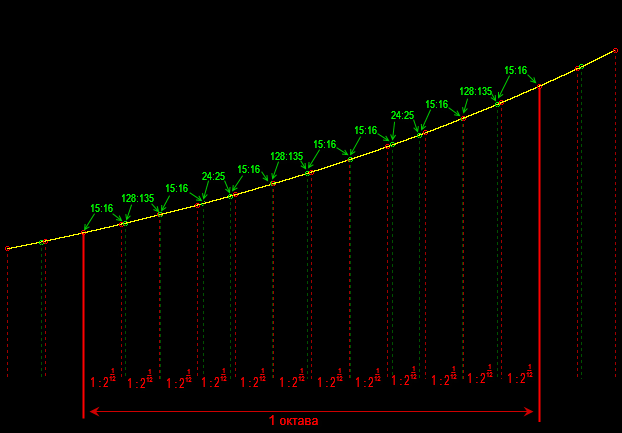
(Красные линии отделяют интервалы равномерно темперированного строя, а красные дроби показывают соотношения частот соседних нот. Зелёные линии и дроби выполняют аналогичную задачу для натурального строя)
Ноты в пределах октавы имеют свои названия, которые присваиваются нотам в определённой последовательности, а эта последовательность повторяется каждую октаву. Одноимённые ноты всегда имеют между собой интервал, равный целому числу октав, и в целом такие ноты считаются одинаковыми с точность до принадлежности к октавам. Выражаясь математическим языком, сравнение нот — это
сравнение по модулю 12.
_________________________
Другой важный факт о современной и не очень музыке: с некоторым упрощением можно сказать: определённые сочетания одновременно звучащих нот оказывают на человека тот или иной психологический эффект. Производимый эффект зависит от интервалов между одновременно звучащими нотами.
Одновременное звучание как минимум трёх неодинаковых (!) нот называется аккордом.
Есть в музыке такое понятие, как «гармония», которое имеет тысячу значений, одно из которых — последовательность созвучий. И сами созвучия, и их последовательность при этом подчинены некоторым закономерностям. Если упростить и выкинуть из рассмотрения некоторые нестандартные и экзотические вещи, можно грубо сказать, что если рассматривать какое-то произведение, то помимо мелодической линии в нём явно или неявно присутствует последовательность аккордов, в подчинении которой находятся так или иначе все партии произведения. Нередко эти аккорды сами являются самостоятельной партией в произведении.
__________________________
К сожалению, пришлось рассказать кучу вещей, хотя и их пришлось упростить, иначе дальнейший рассказ имел бы смысл только для, возможно, пары человек, которые и так всё это знали.
_________________________
Классический анализатор спектра делает FFT (или не FFT, но это не так существенно сейчас) и отображает полученный результат в виде графика в прямоугольной системе координат:
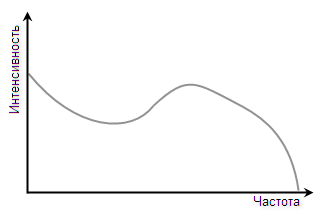
X-координата означает частоту, Y-координата — интенсивность. Я специально написал слово «интенсивность», а не, к примеру, «амплитуда», потому что в общем случае это именно интенсивность, которая может означать и амплитуду, и среднеквадратическую мощность спектральной составляющей, и уровень в децибелах и что-нибудь ещё.
Что касается горизонтальной оси, означающей частотную область, может применяться либо линейный масштаб:
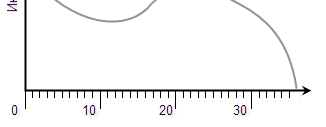
Либо логарифмический:
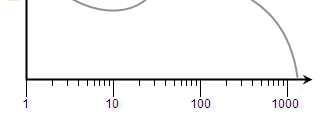
Нас, понятное дело, интересует логарифмический масштаб, потому что при нём любая октава, тон или полутон или центр (цент — одна сотая полутона равномерно темперированного строя) имеют одинаковую ширину на графике.
Итак, моя изначальная идея предельно проста:
Использовать логарифмический масштаб, но вместо декартовых координат использовать полярные.То, что в декартовых координатах было
x-координатой, — станет угловой координатой.
То, что в декартовых координатах было
y-координатой, — станет радиальной координатой.
Иными словами, радиальная координата будет пропорциональна интенсивности, а углавая координата — логарифму частоты спектральной составляющей по основанию 2. Причём для угловой координаты коэффициент пропорциональности
должен быть выбран таким, чтобы на один оборот приходилась одна октава.
Это абсолютный минимум изложения моей идеи, потому что дальше у неё есть развитие и сопутствующие ограничения и требования, но пока ограничимся этим.
Что это даёт?
Музыкальные интервалы превращаются в углы!
Полутон превращается в 30°, тон — в 60°. Цент — в 0.3°.
Октава превращается в полный оборот — 360°.
Нота «До» самой низкой октавы и нота «До» самой высокой октавы (равно как и нота «До» вообще любой октавы) в полярных координатах соответствует лучу имеющиму один и тот же угол наклона, и соответственно все эти ноты отображаются одинаково.
На данном этапе этот фактор (одинаковые ноты разных октав накладываются и сливаются в одну при полярном отображении) может рассматривать как недостаток такого способа отображения, но подождите, об этом будет сказано дальше.
Пока же — маленький пример.
Спектр органа (звучит нота «До»):
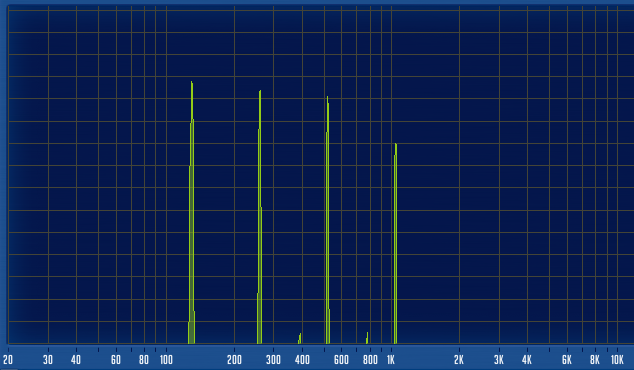
На этой спектрограмме хорошо видно базовый тон и обертоны. Причём видно, что интенсивность 1-го,3-го и 7-го обертонов — высокая, а интенсивность 2-го, 4-го, 5-го, 6-го, 8-го и последующих обертонов — или незначительная, или неразличимо малая.
Фактически, мы вы видим четыре гармоники (гармоника — спектральная составляющая), отстающие друг от друга на одну октаву.
Если бы мы смотрели на спектр огранного звука в спектральном анализаторе, использующим полярные координаты для частоты, мы бы увидели 4 наложившихся друг на друга лепестка.
Что касается термина «лепесток». В некоторых кругах это весьма знакомый и часто-используемый термин, причём как в отношении полярных координат, так и прямоугольных.
Вообще же на идею использования полярных координат меня подтолкнула совокупность двух вещей:
- Осознание особой роли такого интервала, как «октава», осознание того факта, что среди ряда обертонных гармоник многие частоты отстают друг от друга ровно на октаву, а у тембров некоторых инструментов (например органа) все гармоники только и сидят на октавной сетке.
- Плотное знакомство и частое рассматривание диаграмм направленности/восприимчивости (антенн, излучателей, приёмников).
Вот например, диаграмма направленности антенны:
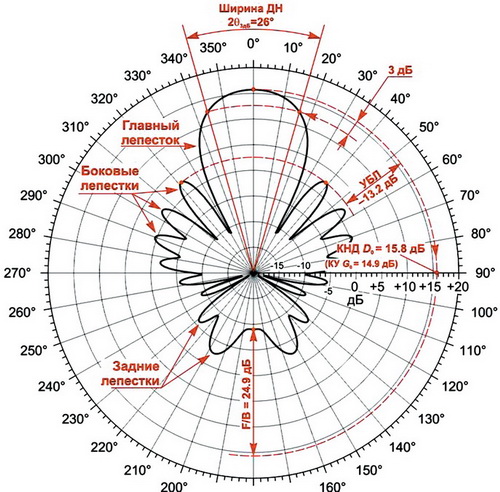
Надеюсь, после этой картинки как минимум понятно, что подразумевается под термином «лепесток».
Теперь вернёмся к спектру органа. Те четыре гармоники, которые в нём присутствуют (слабо проявляющиеся — не рассматриваем), на полярном анализаторе будут выглядеть вот так:
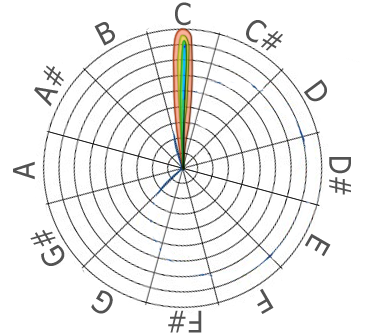 (Латинские обозначения: стандартные латинские обозначения нот — буква «A»
(Латинские обозначения: стандартные латинские обозначения нот — буква «A»
для «Ля» и далее по алфавиту до следующей ноты «Ля».
Один сектор соответствует одному полутону).
Красиво, правда?
Теперь очень важный момент.Выше я отметил, что если бы лепестки просто накладывались друг на друга, это было бы не очень хорошо: мы бы потеряли много информации, в частности, не смогли бы отличить ноту, играемую бедным синусным тембром от той же ноты, играемой органным тембром.
Поэтому важная вещь, которую я хочу постулировать: особые правила отображения наложения лепестков.
Они состоят из двух пунктов:
- Лепестки не имеют одинакового цвета. Цвет лепестка зависит от частоты (т.е. высоты тона). Таким образом частота влияет не только на угловую координату, но и на цвет лепестка.
- Лепестки не являются непрозрачными. Прозрачность лепестка должна иметь зависимость от интенсивности спектральной составляющей. Я не говорю о том, что это должна быть полная зависимость, но должен существовать определённый весовой коэффициент, устанавливающий такую зависимость. Приветствуется возможность изменять этот весовой коэффициент.
- Особое правило цветового наложения: поскольку лепестки полупрозрачны, в местах наложения лепестков конечный цвет точки должен определяться по аддитивным правилам синтеза цвета. Не стоит путать это обычным наложением полупрозрачных цветовых слоёв: при простом наложении порядок следования слоёв играет роль, в то время как при аддитивном сложении (простите за такую тавтологию) цветовые операнды, так сказать, коммутативны, т.е. порядок слагаемых не играет никакой роли. Таким образом, базовый тон одной и той же ноты, но сыгранной в разных октавах, будет иметь лепесток разных цветов. Важное правило: если сыграть одну и ту же ноту во всех октавах из слышимого для человека диапазона — в результате сложения лепестков должен получиться белый лепесток.
- Синергический эффект лепестков: для всего всего кругового пространства должен быть подсчитан как я его называю «синергический коэффициент». Чем большее количество гармоник приходится на данную угловую координату и чем интенсивнее каждая из них, тем больше синергический коэффициент в данной точки. В конце концов радиальный размер всех лепестков при отображении умножается на этот коэффициент. В результате получается, что гармоники, соответствующие одной и той же ноте и звучащие сразу в нескольких октавах, при отображении будут сильно выделяться относительно близких гармоник, которые звучат только в одной октаве. Эта фишка отображения должна быть опциональной (включаемой/выключемой) и вклад интенсивности и зависимость вклада от частоты, и вообще вклад синергического коэффициента в общую картину должен тщательно подбираться весовыми коэффициентами, иначе эта фишка принесёт больше неразберихи, нежели пользы.
Касательно зависимости цвета лепестка от частоты: очевидно должны быть какие-либо формулы или кривые, выполняющие функцию сопоставления RGB- или HSB-значений частоте. Очевидно, что HSB тут значительно удобнее: можно привязать H-компоненту к частоте. Но на самом деле, нужно тщательно поизучать цветовые модели, модели смешения цветов и выбрать оптимальный вариант: оптимальный — значит такой, чтобы получать белый цвет именно тогда, когда это нужно. Вероятно, нужно цвета в цветовом пространстве представлять векторами, складывать эти векторы а потом нормализовать результирующий вектор.
В целом зависимость частоты и цвета должна быть примерно такой, какой является зависимость цвета от температуры в тепловизорах:

.
Один интересный побочный эффект особенностей FFT: частотное разрешение падает с уменьшением частоты. Благодаря этому, лепестки не будут полностью перекрываться: НЧ-лепестки будут шире (в плане углового размера) ВЧ-лепестков. С ростом частоты, при прочих равных, ширина лепестков будет уменьшаться. Поэтому в любых случаях, белая сердцевина, полученная в результате многократных наложений лепестков, будет видна только в самом центре скопления лепестков — вдоль их оси, в то время как вокруг этой оси будет хорошо видна послойная структура всех лепестков (посмотрите ещё раз на мой самодельный рисунок (сделан в фотошопе) выше — красный лепесток наиболее широк, синий — наиболее узок).
Таким образом, с учётом разницы ширины лепестков и механизмом сложения цвета, отображение планируется примерно таким:
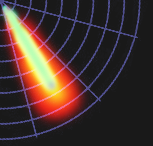 (Опять же: концепт-арт в Фотошопе)Что в целом даёт такой подход?
(Опять же: концепт-арт в Фотошопе)Что в целом даёт такой подход?Вместо гармоник вы видите ноты. Вместо интервалов — углы. Вместо аккордов — фигуры из лепестков.
Немного об аккордах. Как я уже писал выше, классификация аккордов поразит вас своей объёмностью. Из всего этого безобразия можно взять небольшой пласт самых простых аккордов — трезвучия.
Не любые три одновременно звучащие ноты называются трезвучиями, а только те, которые состоят из трёх нот, интервалы между которыми (если отбросить один момент о котором — пару абзацев ниже) между которыми являются терциями. Вообще-то нет такого интервала как «терция», а есть несколько разновидностей
терции. Нас же интересуют малая терция — интервал в три полутона, и большая терция — интервал в четыре полутона.
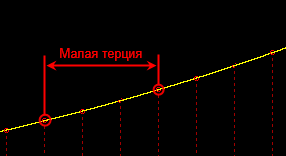
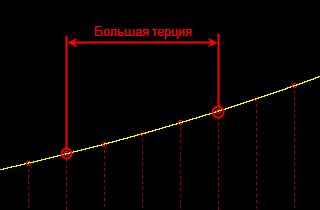
Напомню ещё раз, что это интервал между
любыми двумя нотами, не важно — какими. Поскольку мы условились делить октаву на 12 равных интервальных частей, которые мы называем полутонами, не играет роли, какие абсолютны значения имеют частоты базовых тонов двух сравниваемых нот. Играет роль только их относительное соотношение. Поскольку полутон — это отношение 1 : 2
1/12, малая терция — это соотношение 1 : 2
3/12, а большая терция — соотношение 1 : 2
4/12.
«В лучших традициях» комбинаторики, имея два варианта терции, мы получаем 4 возможных комбинации из этих двух интервалов:
- Большая терция + малая терция = Мажорное трезвучие:
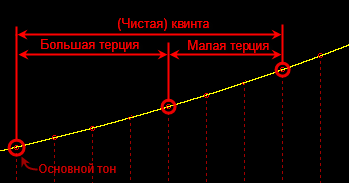
- Малая терция + большая терция = Минорное трезвучие:
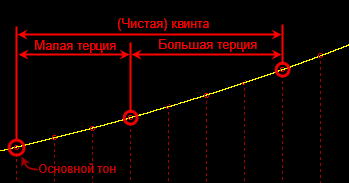
- Большая терция + большая терция = Увеличенное трезвучие
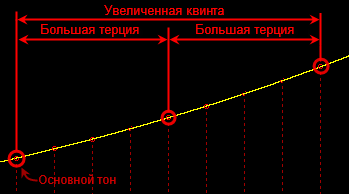
- Малая терция + Малая терция = Уменьшенное трезвучие
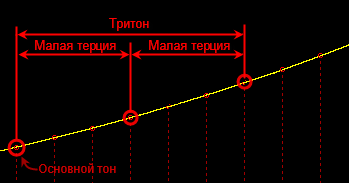
Причём первые два используются значительно чаще, чем вторые два, потому что первые два считаются консонирующими (благозвучными), а вторые два — диссонирующими (т.е. неблагозвучными, вызывающими ощущение диссонанса). Это свойство последних двух часто используется чтобы создать момент напряженности в произведении.
Считается, что мажорное трезвучие звучит радостно, а минорное — грустно. Даже слова «мажорный» и «минорный», как я погляжу, стали синонимами слов «радостный» и «грустный». Хотя на самом же деле это просто латинские слова major и minor, переводящиеся как «больший» и «меньший» соответственно, и они просто показывают, с какой терции (большой или малой) начинается построение трезвучия. Что же касается радостного и грустного звучания, то можно радостное произведение построить из подавляющего большинства минорных аккордов, и наоборот, так что если и говорит об эмоциональной окраске аккорда, то это «окраска в вакууме».
Аккордам дают название в соответствии с названием ноты, которая послужила базовой для построения аккорда (от которой была отложена сначала одна терция, а затем ещё одна). Например: До-минор или Фа-мажор. В латинской же системе мажорные аккорды обозначаются той же буквой, что и основной тон, а минорные — буквой ноты, ставшей основным тоном аккорда, с добавлением строчной буквы «m». Например
Cm и
F.
Теперь вернёмся к полярной системе координат. Терции преобразуются в углы:
Малая терция — прямой угол (90°).
Большая терция — угол 120 °.
Трезвучиям, в свою очередь, будут соответствовать комбинации из лепестков:
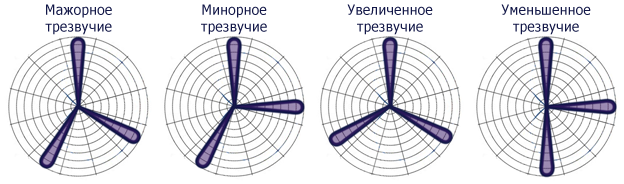
Важные свойства:
- От какой бы ноты ни был построен аккорд, он всегда сохраняет свою конфигурацию лепестков и при смене основного тона аккорда происходит только вращение трёхлепесткового блока вокруг центра. Углы сохраняются.
- Если какие-то ноты (или все ноты) аккорда будут продублированы в других октавах, это не исказит визуализацию аккорда.
Теперь кое-что об аккордах, потому что не-специалисты не знают.
Есть такое явление (и понятие) как
обращения аккордов.
- Вы можете самую низкую ноту аккорда перенести на октаву вверх.
- Или самую верхнюю ноту аккорда перенести на октаву вниз.
Эта манипуляция может быть проделаны несколько раз. Ключевой момент обращений: обращения несколько меняют звучания, но они не меняют аккорда и его названия по сути (Ре-минор останется ре-минором).
Три подряд выполненных обращения дают изначальный аккорд, но перенесённый на октаву вниз или на октаву вверх.
Обращения аккорда «До-минор» на примере сетки полутонов и клавиатуры:
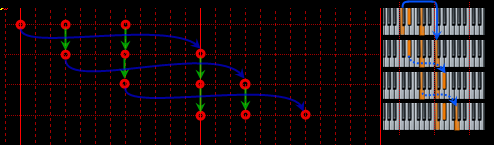
Аналогичным, но зеркальным образом осуществляется обращение вниз.
Обращение в некоторой степени меняет характер звучания, но никогда не делает из мажора минор, из минора — мажор или какие-либо подобные преобразования. Аккорд остаётся принципиально тем же, чем он был.
Важное свойство аккордов в отношении полярного отображения спектра: все обращения некоторого аккорда имеют идентичную геометрическую форму (комбинацию углов между лепестками). При обращении аккордов лепестки не двигаются, углы не меняются,, но меняется цвет лепестков.Теперь немного практики:
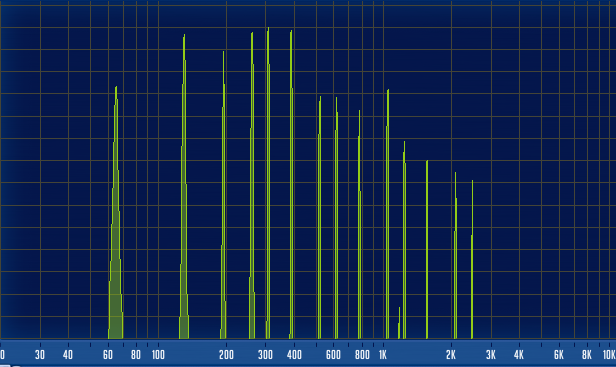
Какие ноты здесь играют? Если отбросить октавное дублирование, сколько нот здесь играет одновременно? Если там аккорд, то какой?
Уверен, быстрым взглядом, глядя на спектр, нельзя дать ответы на эти вопросы: гораздо проще будет положиться на слух, нежели на картинку.
Но с полярным спектроанализатором мы увидим, что это аккорд «До-минор», претерпевший одно обращение вниз, плюс сыгранная в басу нота «До»:
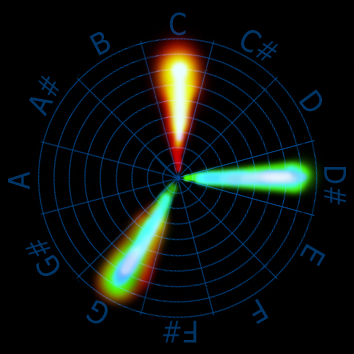 (Это всего лишь неважно получившийся набросок предполагаемого вида: резкость границ лепестков не обязательно должна быть такой мутной — это всё как минимум «под вопросом», а как максимум — должно легко твикаться настройкой спектроанализатора).
(Это всего лишь неважно получившийся набросок предполагаемого вида: резкость границ лепестков не обязательно должна быть такой мутной — это всё как минимум «под вопросом», а как максимум — должно легко твикаться настройкой спектроанализатора).Подытожу некоторые ключевые моменты и требования к анализатор, соответствующему моей концепции:
- Полярные координаты вместо декартовых. А вообще-то анализатор должен иметь переключатель для выбора между прямоугольной и полярной системами координат.
- Спектральные компоненты должны отображаться в виде лепестков, а не столбцов в прямоугольном режиме и секторов в полярном.
- В полярном режиме: один оборот — одна октава.
- Обязательное соответствие цвета лепестка частоте, которую лепесток отождествляет.
- Обязательно сложный принцип синтеза цветов при наложении лепестков.
- Как вариант расположение спектральной компоненты в стерео-пространстве может вносить вклад в цвет лепестка тоже.
- Включаемый по желанию пользователя принцип синергии гармоник.
- Куча крутилок для твикинга всего отображения.
- Мощная сетка-оверлей, делящая окружность на сектора-интервалы. По дефолту секта должна быть настроена на 12-интервальный равномерно темперированный строй с опорной частотой 440 Гц. Ноты должен быть подписаны. По желанию пользователь может выбрать любой другой строй, поменять число интервалов, сменить стиль подписывания нот, сменить опорную частоту. Конфигурируемые субделения, например, для центов.
- Конфигурируемый выбор между достижением максимального временнОго или достижением максимального частотного разрешения.
- Опциональный твикинг параметров FFT и сглаживания полученных данных.
- Маркеры-курсоры, с помощью которых пользователь может ставить метки и делать измерения.
- Анализатор должен быть выполнен в виде VST, чтобы была возможность использовать его в любом хосте (DAW)
_______________
Когда я увидел эту реализацию, я испытывал смешанные чувства. С одной стороны кому-то было не лень воплотить в жизнь мою идею (мне-то всё равно некогда), но с другой стороны, мою идею сильно исказили и оболванили задумку до такого уровня, что такой непривычный вывод стал просто бесполезным и непригодным для чего-то.
Когда я вижу секторы вместо гладких лепестков — у меня из глаз идёт кровь

Когда я вижу, что нет столь важного аддитивного сложения цветов — мне печально.
Но самое главное: совершенно
неприемлемо низкое спектральное разрешение.
Предлагаю сравнить.
Вот скриншот неплохого бесплатного спектрального анализатора Voxengo SPAN, а на его фоне открыл TrickSpectrum. Сперва я в SPAN'е специально включил режим «запоминать максимум», сузил диапазон отображаемого окна до примерно одной октавы и прошёлся по всем полутонам октавы подряд, подовая на вход анализатора ноту, состоящую из одного только синусоидального сигнал. Получилась тёмно-зелёная гребёнка, пики которой соответствует сетке равномерно темперированного строя. Затем я в граф. редакторе подписал полученные ноты.

.
По этому скриншоту хорошо видно, что для каждой ноты в составе равномерно темперированной октавы разрешающей способности SPAN-а хватает, чтобы отобразить ноту как отдельный лепесток. Между двумя соседними нотами можно ещё нечто промежуточное умостить, и это будет видно на спектре.
На момент снятия скриншота звучит нота «До», её видно на спектре как ярко-зелёный лепесток, который не залазит на соседние ноты. Я могу легко определить, не расстроена ли случайно нота «До» на 30 центов вниз или вверх. Разрешения и метод визуализации позволяет.
Если же посмотреть на TrickSpectrum, то видно, что абсолютно та же нота отображается как нечто равное, и занимает (наберите воздуха поглубже) сектор в 2/3 октавы!!!
Это никуда не годится.Это не имеет под собой никакого смысла.
Полярный анализатор спектра должен показывать ту же картину, что и SPAN, только она должна быть как бы обёрнута вокруг точки. Те же лепестки с той же шириной. Те же пропорции ширины лепестков и промежутков между ними.
Хотя это и ужасно само по себе, но я бы даже согласился, если бы одиночную ноту «До» он визуализировал не как изящный лепесток, а как огромный угловый 30°-ный сектор. Чёрт с ним, но 120° на одну ноту — это просто даже словами не выразить, насколько неприемлемо.
В общем, моя идея, которая мне пришла у голову уже очень давно, она подразумевала создание анализатора, которым действительно можно пользоваться, который показывает информацию в том уникальном виде, в котором человек её легко может интерпретировать, в отличие от тех видов, в которых это показывают другие спектроанализаторы и спектро-вьюверы. Я долго искал хотя бы одну реализацию, но не нашёл ни одной.
К сожалению, теперь похоже «первая в истории» утилита для полярного вывода спектра создана, и вроде бы как создана по моей идее, но до того, как она должна по моей задумке (с основной на рассказал о которой это программка и была создана), ей как до Китая пешком, и это обидно.
Анализатор получился неюзабельным в практическом плане: на сколько-нибудь более серьёзном заполненном спектре он показывает просто кашу и хаотически мигающие сектора с неожидаемыми границами. Как развлекательная безделушка это пойдёт, но спектроанализатор пока не удался, тем более тот, идеей которого я поделился — пока не вышел.

















 .
. 











 .
.