.
.
–£–≤—Л, –љ–Њ –Љ–љ–µ –њ–Њ–Ї–∞ –љ–µ –љ—А–∞–≤–Є—В—Б—П.
–Я—А–Є–і—С—В—Б—П –Љ–љ–µ —Б–і–µ–ї–∞—В—М –љ–µ–±–Њ–ї—М—И–Њ–є —Н–Ї—Б–Ї—Г—А—Б –≤ —Г—Б—В—А–Њ–є—Б—В–≤–Њ –Ј–≤—Г–Ї–∞, –Љ—Г–Ј—Л–Ї–Є –Є —Б—Г—В—М –Љ–Њ–µ–є –Є–і–µ–Є.
–Э–µ –±—Г–і—Г —А–∞—Б—Б–Ї–∞–Ј—Л–≤–∞—В—М, —З—В–Њ –ї—О–±–Њ–є –Ј–≤—Г–Ї–Њ–≤–Њ–є —Б–Є–≥–љ–∞–ї (–∞ –≤ –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ вАФ –≤–Њ–Њ–±—Й–µ –ї—О–±–Њ–є —Б–Є–≥–∞–љ–ї, –≤–Њ–≤—Б–µ –љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –Ј–≤—Г–Ї–Њ–≤–Њ–є) –Љ–Њ–ґ–љ–Њ —А–∞–Ј–ї–Њ–ґ–Є—В—М –љ–∞ —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є–µ (—Б—Г–Љ–Љ—Г —Б–Є–љ—Г—Б–Њ–Є–і) –Є –љ–∞ –Њ—Б–љ–Њ–≤–µ —Н—В–Њ–≥–Њ –њ–Њ–ї—Г—З–Є—В—М —Б–њ–µ–Ї—В—А —Б–Є–≥–љ–∞–ї–∞.
–Я–Њ–і–Њ–є–і—С–Љ —Б –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л. –Х—Б–ї–Є –≤—Л –і–∞–ї–µ–Ї–Є –Њ—В –Љ—Г–Ј—Л–Ї–Є –Є/–Є–ї–Є –Њ–±—А–∞–±–Њ—В–Ї–Є —Б–Є–≥–љ–∞–ї–Њ–≤, —В–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –≤—Л —Б–ї—Л—И–∞–ї–Є —В–∞–Ї–Њ–є —В–µ—А–Љ–Є–љ
–Њ–Ї—В–∞–≤–∞, –Є —Б—З–Є—В–∞–µ—В–µ, —З—В–Њ —Н—В–Њ —З—В–Њ-—В–Њ, —З—В–Њ –Љ—Г–Ј—Л–Ї–∞–љ—В—Л —Б–њ–µ—А–≤–∞ –њ—А–Є–і—Г–Љ–∞–ї–Є —Б–µ–±–µ, –∞ –Ј–∞—В–µ–Љ –Њ–±–Њ–Ј–≤–∞–ї–Є —Н—В–Є–Љ —Б–ї–Њ–≤–Њ–Љ. –Э–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ, —Н—В–Њ –Њ–і–љ–∞ –Є–Ј –љ–µ–Љ–љ–Њ–≥–Є—Е –≤–µ—Й–µ–є, –Ї–Њ—В–Њ—А—Г—О –љ–Є–Ї—В–Њ –љ–µ –њ—А–Є–і—Г–Љ–∞–ї (–≤ —З–Є—Б—В–Њ–Љ –≤–Є–і–µ), –∞ –Ї–Њ—В–Њ—А–∞—П —П–≤–ї—П–µ—В—Б—П
–Љ–Є—А–Њ–≤–Њ–є –і–∞–љ–љ–Њ—Б—В—М—О.
–Ъ–∞–Ї, –љ–∞–њ—А–Є–Љ–µ—А, —З–Є—Б–ї–Њ –Я–Є. –Э–Є–Ї—В–Њ –љ–µ –њ—А–Є–і—Г–Љ—Л–≤–∞–ї —З–Є—Б–ї–Њ –Я–Є –≤ —В–Њ–Љ —Б–Љ—Л—Б–ї–µ, —З—В–Њ –љ–Є–Ї—В–Њ –љ–µ —А–∞–Ј–Љ—Л—И–ї—П–ї –≤ —Б—В–Є–ї–µ ¬Ђ—П –Њ–±–і—Г–Љ–∞–ї –Љ–љ–Њ–≥–Њ –≤–∞—А–Є–∞–љ—В–Њ–≤ –Є –≤—Л–±–Є—А–∞—О —Н—В–Њ—В¬ї. –°–∞–Љ–Њ –њ–Њ —Б–µ–±–µ —З–Є—Б–ї–Њ –љ–µ –Є–Ј–Њ–±—А–µ—В–µ–љ–Њ –Ї–µ–Љ-–ї–Є–±–Њ, –∞ —П–≤–ї—П–µ—В—Б—П
–Њ–±—Й–µ–Љ–Є—А–Њ–≤–Њ–є –Є—Б—В–Є–љ–Њ–є. –Х–≥–Њ –Ј–љ–∞—З–µ–љ–Є–µ –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В —З—М–µ–≥–Њ-–ї–Є–±–Њ –∞–≤—В–Њ—А–Є—В–µ—В–љ–Њ–≥–Њ –Љ–љ–µ–љ–Є—П, –љ–µ –Љ–µ–љ—П–µ—В—Б—П —Б —Е–Њ–і–Њ–Љ –≤—А–µ–Љ–µ–љ–Є. –Х–≥–Њ –Ј–љ–∞—З–µ–љ–Є–µ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–Њ –і–Њ –≤–Њ–Ј–љ–Є–Ї–љ–Њ–≤–µ–љ–Є—П —З–µ–ї–Њ–≤–µ–Ї–∞, –±—Г–і–µ—В —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞—В—М –њ–Њ—Б–ї–µ –Є—Б—З–µ–Ј–љ–Њ–≤–µ–љ–Є—П —З–µ–ї–Њ–≤–µ–Ї–∞, –Є –≤ —Ж–µ–ї–Њ–Љ, –Љ–Њ–ґ–µ—В —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞—В—М –±–µ–Ј —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П —Б–∞–Љ–Њ–≥–Њ —З–µ–ї–Њ–≤–µ–Ї–∞.
–Х–і–Є–љ—Б—В–≤–µ–љ–љ–Њ–µ, —З—В–Њ —Б–і–µ–ї–∞–ї —З–µ–ї–Њ–≤–µ–Ї: —Н—В–Њ –љ–∞—И—С–ї –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г –і–ї–Є–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Є –і–Є–∞–Љ–µ—В—А–Њ–Љ, –њ–Њ–љ—П–ї, —З—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –≤—Б–µ–≥–і–∞ –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ –Є –і–∞–ї —Н—В–Њ–Љ—Г —З–Є—Б–ї—Г –љ–∞–Ј–≤–∞–љ–Є–µ. –Ь–Њ–≥ –і–∞—В—М –і—А—Г–≥–Њ–µ –љ–∞–Ј–≤–∞–љ–Є–µ. –Ъ–∞–ґ–і—Л–є —З–µ–ї–Њ–≤–µ–Ї –Љ–Њ–≥ –і–∞—В—М —Б–≤–Њ—С –љ–∞–Ј–≤–∞–љ–Є–µ. –Э–∞–Ј–≤–∞–љ–Є–µ –Љ–Њ–≥–ї–Њ –±—Л –±—Л—В—М –і–∞–љ–Њ –љ–∞ 1000 –ї–µ—В —А–∞–љ—М—И–µ –Є–ї–Є –њ–Њ–Ј–ґ–µ. –Э–Њ —Б–∞–Љ–Њ —З–Є—Б–ї–Њ –Њ—В —Н—В–Њ–≥–Њ –љ–Є–Ї–∞–Ї –љ–µ –Љ–µ–љ—П–µ—В—Б—П. –Ю–љ–Њ —Б–∞–Љ–Њ –Є —Б–≤—П–Ј–∞–љ–љ–∞—П —Б –љ–Є–Љ –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В—М —Б—Г—Й–µ—Б—В–≤—Г–µ—В –≤–љ–µ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –љ–∞–ї–Є—З–Є—П –Њ—В –љ–∞–Ј–≤–∞–љ–Є—П –Є —В–Њ–≥–Њ, –Є–Ј–≤–µ—Б—В–љ–∞ –ї–Є –Ї–Њ–Љ—Г —Н—В–∞ –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В—М.
–Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –і–µ–ї–Њ –Њ–±—Б—В–Њ–Є—В —Б
–Њ–Ї—В–∞–≤–Њ–є.
–Ю–Ї—В–∞–≤–∞ вАФ —Н—В–Њ –њ—А–µ–≤–Њ—Б—Е–Њ–і—Б—В–≤–Њ –≤ –і–≤–∞ —А–∞–Ј–∞. –Я—А–µ–≤–Њ—Б—Е–Њ–і—Б—В–≤–Њ —З–∞—Б—В–Њ—В—Л —З–µ–≥–Њ-—В–Њ, –љ–∞–њ—А–Є–Љ–µ—А —З–∞—Б—В–Њ—В—Л —Б–Є–≥–љ–∞–ї–∞. ¬Ђ–Э–∞ –Њ–Ї—В–∞–≤—Г –≤—Л—И–µ¬ї –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –Њ–і–Є–љ —З–∞—Б—В–Њ—В–∞ –Њ–і–љ–Њ–≥–Њ —Б–Є–≥–љ–∞–ї–∞ –±–Њ–ї—М—И–µ —З–∞—Б—В–Њ—В—Л –і—А—Г–≥–Њ–≥–Њ —А–Њ–≤–љ–Њ
–≤ –і–≤–∞ —А–∞–Ј–∞. ¬Ђ–Э–∞ –Њ–Ї—В–∞–≤—Г –љ–Є–ґ–µ¬ї вАФ –Ј–љ–∞—З–Є—В –≤ –і–≤–∞ —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ.
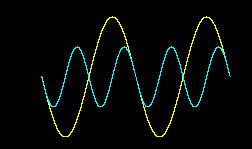 (–≥–Њ–ї—Г–±–Њ–є —Б–Є–≥–љ–∞–ї –љ–∞ 1 –Њ–Ї—В–∞–≤—Г –≤—Л—И–µ –ґ–µ–ї—В–Њ–≥–Њ)
(–≥–Њ–ї—Г–±–Њ–є —Б–Є–≥–љ–∞–ї –љ–∞ 1 –Њ–Ї—В–∞–≤—Г –≤—Л—И–µ –ґ–µ–ї—В–Њ–≥–Њ)–Ы—О–і–Є –њ—А–Њ—Б—В–Њ –Њ–±–љ–∞—А—Г–ґ–Є–ї–Є –Њ—Б–Њ–±–Њ–µ —Б–≤–Њ–є—Б—В–≤–Њ —В–∞–Ї–Њ–≥–Њ —Б–Њ—З–µ—В–∞–љ–Є—П —З–∞—Б—В–Њ—В (–њ—А–Є —В–∞–Ї–Њ–Љ —Б–Њ—З–µ—В–∞–љ–Є–Є —З–∞—Б—В–Њ—В –њ–µ—А–Є–Њ–і—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є –Њ–Ї–∞–Ј—Л–≤–∞—О—В—Б—П –Ї—А–∞—В–љ—Л–Љ–Є, –њ—А–Є—З—С–Љ –љ–∞—Б—В—Г–њ–ї–µ–љ–Є–µ —Г –Њ–±–Њ–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤ –Њ–і–љ–Њ–є —Д–∞–Ј—Л –њ—А–Њ–Є—Б—Е–Њ–і–Є—В –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ —З–∞—Б—В–Њ (–і–ї—П —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П —З–∞—Б—В–Њ—В 1:2 –Љ—Л –Є–Љ–µ–µ–Љ –Љ–Є–љ–Є–Љ–∞–ї—М–љ—Л–є –Э–Ю–Ъ –і–ї—П –њ–µ—А–Є–Њ–і–Њ–≤ –Ї–Њ–ї–µ–±–∞–љ–Є–є)) –Є —А–µ—И–Є–ї–Є —В–∞–Ї–Њ–µ —Б–Њ—З–µ—В–∞–љ–Є–µ —З–∞—Б—В–Њ—В –Ї–∞–Ї-—В–Њ –љ–∞–Ј–≤–∞—В—М. –Ш –љ–∞–Ј–≤–∞–ї–Є –Њ–Ї—В–∞–≤–Њ–є.
–Э–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ, –Є—Б—В–Њ—А–Є—П –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Г–њ—А–Њ—Й–µ–љ–∞, –Є –≤ —Б–ї–Њ–≤–µ –Њ–Ї—В–∞–≤–∞ –Љ—Л –Љ–Њ–ґ–µ—В–µ –љ–∞–є—В–Є –ї–∞—В–Є–љ—Б–Ї–Є–є –Ї–Њ—А–µ–љ—М oct, –Ї–Њ—В–Њ—А—Л–є –Њ–Ј–љ–∞—З–∞–µ—В —З–Є—Б–ї–Њ 8, –љ–Њ —Н—В–Њ –≤—Б—С –љ–µ—Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–µ –і–µ—В–∞–ї–Є.–Ш—В–∞–Ї, –Њ–Ї—В–∞–≤–∞ вАФ —Н—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —З–∞—Б—В–Њ—В –Ї–∞–Ї 1:2. –Х—Б–ї–Є –Њ–і–љ–∞ —З–∞—Б—В–Њ—В–∞ –±—Г–і–µ—В –≤ 8 —А–∞–Ј –±–Њ–ї—М—И–µ –і—А—Г–≥–Њ–є, —В–Њ –Њ–љ–∞ –±—Г–і–µ—В –≤—Л—И–µ ¬Ђ–љ–∞ —В—А–Є –Њ–Ї—В–∞–≤—Л¬ї. –°–Є–љ—Г—Б–Њ–Є–і–∞–ї—М–љ—Л–є —Б–Є–≥–љ–∞–ї —Б —З–∞—Б—В–Њ—В–Њ–є 5 –≥–µ—А—Ж (–Ї–Њ—В–Њ—А—Л–є –≤—Л –і–∞–ґ–µ –љ–µ —Г—Б–ї—Л—И–Є—В–µ, –Є–±–Њ —Н—В–Њ –Є–љ—Д—А–∞–Ј–≤—Г–Ї) –љ–∞ —Б–µ–Љ—М –Њ–Ї—В–∞–≤ –љ–Є–ґ–µ, —З–µ–Љ —В–Њ—В –ґ–µ —Б–Є–љ—Г—Б 640 –У—Ж. –Р —Б–Є–љ—Г—Б–Њ–Є–і–∞–ї—М–љ—Л–є —Б–Є–≥–љ–∞–ї —Б —З–∞—Б—В–Њ—В–Њ–є 666 –У—Ж –љ–∞ –Њ–і–љ—Г –Њ–Ї—В–∞–≤—Г –≤—Л—И–µ, —З–µ–Љ —Б–Є–љ—Г—Б–Њ–Є–і–∞–ї—М–љ—Л–є —Б–Є–≥–љ–∞–ї —З–∞—Б—В–Њ—В–Њ–є 333 –У—Ж.
–Я–Њ —Б—Г—В–Є, –Њ–Ї—В–∞–≤–∞ вАФ —Н—В–Њ –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ–∞—П –µ–і–Є–љ–Є—Ж–∞ –і–ї—П –≤—Л—А–∞–ґ–µ–љ–Є—П
–Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–є —А–∞–Ј–љ–Є—Ж—Л –і–≤—Г—Е —З–∞—Б—В–Њ—В. –Ґ–Њ—З–љ–Њ —В–∞–Ї–∞—П –ґ–µ, –Ї–∞–Ї
–і–µ—Ж–Є–±–µ–ї —П–≤–ї—П–µ—В—Б—П –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ–Њ–є –µ–і–Є–љ–Є—Ж–µ–є –і–ї—П –≤—Л—А–∞–ґ–µ–љ–Є—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–є —А–∞–Ј–љ–Є—Ж—Л –і–≤—Г—Е —Г—А–Њ–≤–љ–µ–є. –Х–і–Є–љ–Є—Ж–∞–Љ–Є –і–ї—П –≤—Л—А–∞–ґ–µ–љ–Є—П –∞–±—Б–Њ–ї—О—В–љ–Њ–є —А–∞–Ј–љ–Є—Ж—Л –±—Л–ї–Є –±—Л, –Ї –њ—А–Є–Љ–µ—А—Г, –≥–µ—А—Ж—Л –Є –≤–Њ–ї—М—В—Л (–Є–ї–Є –≤–∞—В—В—Л, –Є–ї–Є —З—В–Њ-—В–Њ –µ—Й—С) —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Ъ–∞–Ї –Є –≤ —Б–ї—Г—З–∞–µ —Б –і–µ—Ж–Є–±–µ–ї–∞–Љ–Є, –Ј–і–µ—Б—М –≤—Б—С –Ї—А—Г—В–Є—В—Б—П –≤–Њ–Ї—А—Г–≥ –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Њ–є —И–Ї–∞–ї—Л: –µ—Б–ї–Є –Ї–∞–Ї–Є–µ-–ї–Є–±–Њ –≤–µ–ї–Є—З–Є–љ—Л –Њ—В–Љ–µ—З–∞—В—М —В–Њ—З–Ї–∞–Љ–Є –љ–∞ —И–Ї–∞–ї–µ —Б –ї–Є–љ–µ–є–љ—Л–Љ –Љ–∞—Б—И—В–∞–±–Њ–Љ, —В–Њ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –ї—О–±—Л–Љ–Є —В–Њ—З–Ї–∞–Љ–Є –±—Г–і—Г—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ —В–Њ–Љ—Г
–љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ –Њ–і–љ–∞ –±–Њ–ї—М—И–µ –і—А—Г–≥–Њ–є, –≤ —В–Њ –≤—А–µ–Љ—П, –Ї–∞–Ї –µ—Б–ї–Є —В–µ –ґ–µ –≤–µ–ї–Є—З–Є–љ—Л –Њ—В–Љ–µ—З–∞—В—М —В–Њ—З–Ї–∞–Љ–Є –љ–∞ —И–Ї–∞–ї–µ —Б –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Є–Љ –Љ–∞—Б—И—В–∞–±–Њ–Љ вАФ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –ї—О–±—Л–Љ–Є –і–≤—Г–Љ—П —В–Њ—З–Ї–∞–Љ–Є –±—Г–і–µ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ —В–Њ–Љ—Г,
–≤–Њ —Б–Ї–Њ–ї—М–Ї–Њ —А–∞–Ј –Њ–і–љ–∞ –≤–µ–ї–Є—З–Є–љ–∞ –±–Њ–ї—М—И–µ –і—А—Г–≥–Њ–є.
–Х—Б–ї–Є f1 –љ–∞ n –Њ–Ї—В–∞–≤ –≤—Л—И–µ, —З–µ–Љ f2, –Ј–љ–∞—З–Є—В f1 = f2 √Ч 2n–Ъ–∞–Ї –≤—Л –њ–Њ–љ–Є–Љ–∞–µ—В–µ, –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М —Б—В–µ–њ–µ–љ–Є –љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–ї–ґ–µ–љ –±—Л—В—М —Ж–µ–ї—Л–Љ, –њ–Њ—Н—В–Њ–Љ—Г –Є–љ—В–µ—А–≤–∞–ї –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П —В–Њ–љ–∞–Љ–Є –љ–µ –Њ–±—П–Ј–∞–љ –Є–Ј–Љ–µ—А—П—В—М—Б—П —Ж–µ–ї—Л–Љ —З–Є—Б–ї–Њ–Љ –Њ–Ї—В–∞–≤. –°–Є–љ—Г—Б–Њ–Є–і–∞–ї—М–љ—Л–є —Б–Є–≥–љ–∞–ї —З–∞—Б—В–Њ—В–Њ–є 200 –У—Ж –љ–∞ –і–≤–µ –Њ–Ї—В–∞–≤—Л –≤—Л—И–µ, —З–µ–Љ —Б–Є–≥–љ–∞–ї 50 –У—Ж, –љ–Њ –љ–∞ 1.5 –Њ–Ї—В–∞–≤—Л –љ–Є–ґ–µ, —З–µ–Љ —Б–Є–≥–љ–∞–ї 565.7 –У—Ж.
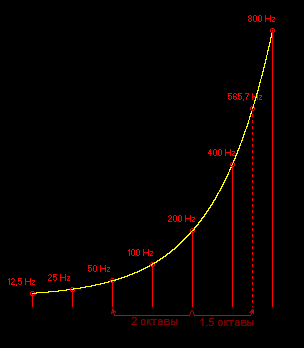
–Ю–±—А–∞—В–љ–Њ–µ:
–Х—Б–ї–Є –і–≤–∞ —В–Њ–љ–∞ –Є–Љ–µ—О—В —З–∞—Б—В–Њ—В—Л f1 –Є f2, –Ј–љ–∞—З–Є—В –Є–љ—В–µ—А–≤–∞–ї –Љ–µ–ґ–і—Г –љ–Є–Љ–Є –≤ –Њ–Ї—В–∞–≤–∞—Е: n = log2(f2) вАУ log2(f1) = log2(f2 / f1)–Ш—В–∞–Ї, –Њ–Ї—В–∞–≤–∞ вАФ –Њ–і–љ–∞ –Є–Ј –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ –љ–µ–Љ–љ–Њ–≥–Є—Е –≤–µ—Й–µ–є –≤ –Љ—Г–Ј—Л–Ї–µ, –Ї–Њ—В–Њ—А—Г—О –ї—О–і–Є –љ–µ —Б–∞–Љ–Є –њ—А–Є–і—Г–Љ–∞–ї–Є –Є –њ—А–Є–≤–љ–µ—Б–ї–Є –≤ —Б–≤–Њ—О –љ–∞—Г–Ї—Г, –∞ –Ї–Њ—В–Њ—А—Г—О –Њ–љ–Є –њ—А–Њ—Б—В–Њ –Ј–∞–Љ–µ—В–Є–ї–Є (–Ї–∞–Ї –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В—М) –Є –і–∞–ї–Є –µ–є –Ї–∞–Ї–Њ–µ-—В–Њ –Є–Љ—П. –Ш–Ј –ї—О–±—Л—Е –і–≤—Г—Е —Б–Њ—З–µ—В–∞–љ–Є–є –і–≤—Г—Е –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –Ј–≤—Г—З–∞—Й–Є—Е —В–Њ–љ–Њ–≤, –±–Њ–ї—М—И–Є–љ—Б—В–≤–Њ —Б–Њ—З–µ—В–∞–љ–Є–є –Ј–≤—Г—З–Є—В –њ—А–Њ—Б—В–Њ –Њ—В–≤—А–∞—В–Є—В–µ–ї—М–љ–Њ, –љ–µ–Ї–Њ—В–Њ—А—Л–µ —Б–Њ—З–µ—В–∞–љ–Є—П –і–∞—О—В ¬Ђ–Є–љ—В–µ—А–µ—Б–љ—Л–µ¬ї –Ј–≤—Г—З–∞–љ–Є—П, –≤ –Ї–Њ—В–Њ—А—Л—Е —Б–ї—Л—И–∞—В—Б—П –і–≤–∞ –Ј–≤—Г—З–∞—Й–Є—Е —В–Њ–љ–∞, –Є –ї–Є—И—М –і–≤–∞ —В–Њ–љ–∞, –Є–љ—В–µ—А–≤–∞–ї –Љ–µ–ґ–і—Г –Ї–Њ—В–Њ—А—Л–Љ–Є —Б–Њ—Б—В–∞–≤–ї—П–µ—В –Њ–Ї—В–∞–≤–∞ (–ї–Є–±–Њ –Ї—А–∞—В–µ–љ –Њ–Ї—В–∞–≤–µ) –Ј–≤—Г—З–∞—В –Ї–∞–Ї –Њ–і–Є–љ —В–Њ–љ, –љ–Њ –±–Њ–ї–µ–µ ¬Ђ–ґ–Є—А–љ—Л–є¬ї. –Х—Б–ї–Є –Њ—В –њ—Б–Є—Е–Њ-–∞–Ї–Ї—Г—Б—В–Є—З–µ—Б–Ї–Њ–≥–Њ –≤–Њ—Б–њ—А–Є—П—В–Є—П –њ—А–Њ–≤–µ—Б—В–Є –∞–љ–∞–ї–Њ–≥–Є—О –Ї –≥—А–∞—Д–Є—З–µ—Б–Ї–Њ–Љ—Г: —В–∞–Ї–Є–µ —В–Њ–љ–∞ –≤–Њ—Б–њ—А–Є–љ–Є–Љ–∞—О—В—Б—П –Ї–∞–Ї –њ–Њ–і–Њ–±–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є, –Њ—В–ї–Є—З–∞—О—Й–Є–µ—Б—П —Б–≤–Њ–Є–Љ–Є —А–∞–Ј–Љ–µ—А–∞–Љ–Є, –љ–Њ –љ–µ —Д–Њ—А–Љ–Њ–є.
–Ф–∞–ї—М—И–µ –љ–∞—З–Є–љ–∞–µ—В—Б—П —Ж–∞—А—Б—В–≤–Њ —Б–Њ–≥–ї–∞—И–µ–љ–Є–є.
–Ь—Г–Ј—Л–Ї–∞ —А–Њ–і–Є–ї–∞—Б—М –і–ї—П —З–µ–ї–Њ–≤–µ—З–µ—Б—В–≤–∞ —А–∞–љ—М—И–µ –Љ–љ–Њ–≥–Є—Е –≤–µ—Й–µ–є, —А–∞–љ—М—И–µ –њ–Є—Б—М–Љ–µ–љ–љ–Њ—Б—В–Є, –Љ–Њ–ґ–µ—В –±—Л—В—М –і–∞–ґ–µ —А–∞–љ—М—И–µ —А–µ—З–Є. –Я–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ —З–µ–ї–Њ–≤–µ—З–µ—Б—В–≤–Њ –і–ї—П –Ј–≤—Г–Ї–Њ–Є–Ј–≤–ї–µ—З–µ–љ–Є—П –њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Њ—Б—М —В–µ–Љ, —З—В–Њ –њ–Њ–і —А—Г–Ї–Њ–є, —З–µ—А–µ–Ј –Ї–∞–Ї–Њ–µ-—В–Њ –≤—А–µ–Љ—П –ї—О–і–Є –љ–∞—З–∞–ї–Є –Ї–Њ–љ—Б—В—А—Г–Є—А–Њ–≤–∞—В—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В—Л –≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–Є —Б–Њ —Б–≤–Њ–Є–Љ–Є —В—А–µ–±–Њ–≤–∞–љ–Є—П–Љ–Є. –Ю—В–±—А–Њ—Б–Є–Љ –Є–љ—Б—В—А—Г–Љ–µ–љ—В—Л, –Ї–Њ—В–Њ—А—Л–µ –Є–Ј–і–∞—О—В –≤—Б–µ–≤–Њ–Ј–Љ–Њ–ґ–љ—Л–µ —И—Г–Љ—Л, —В–Њ –µ—Б—В—М –Ј–≤—Г–Ї–Є, —Б–њ–µ–Ї—В—А –Ї–Њ—В–Њ—А—Л—Е —Б–Њ—Б—В–Њ–Є—В –Є–Ј –Ї–Њ–љ–Ї—А–µ—В–љ—Л—Е ¬Ђ—В–Њ–Љ–Њ–≤¬ї, –∞ –Є–Ј –Њ–≥—А–Њ–Љ–љ–Њ–≥–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є—Е –≤—Б–µ—Е –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е —З–∞—Б—В–Њ—В.
–Т–Њ–Ј—М–Љ—С–Љ —Б–∞–Љ—Л–є –њ—А–Њ—Б—В–Њ –њ—А–Є–Љ–µ—А: –њ–µ–љ—М —Б —Й–µ–њ–Ї–Њ–є.
 (–Ї–∞–і—А –Є–Ј –Љ—Г–ї—М—В—Д–Є–ї—М–Љ–∞ ¬Ђ–Т–µ—А—И–Ї–Є –Є –Ї–Њ—А–µ—И–Ї–Є¬ї)
(–Ї–∞–і—А –Є–Ј –Љ—Г–ї—М—В—Д–Є–ї—М–Љ–∞ ¬Ђ–Т–µ—А—И–Ї–Є –Є –Ї–Њ—А–µ—И–Ї–Є¬ї)–Ь–µ—В–Њ–і–Є–Ї–∞ –Є–Ј–≤–ї–µ—З–µ–љ–Є—П –Ј–≤—Г–Ї–∞ –Є–Ј —Й–µ–њ–Ї–Є –њ—А–Њ—Б—В–∞: –≤—Л, –њ—А–Є–Ї–ї–∞–і—Л–≤–∞—П —Г—Б–Є–ї–Є–µ, –Њ—В—В—П–≥–Є–≤–∞–µ—В–µ –Ї–Њ–љ–µ—Ж —Й–µ–њ–Ї–Є –љ–∞ –Ї–∞–Ї–Њ–µ-—В–Њ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Є –Њ—В–њ—Г—Б–Ї–∞–µ—В–µ –µ–≥–Њ. –Я–Њ–і –і–µ–є—Б—В–≤–Є–µ–Љ —Б–Є–ї—Л —Г–њ—А—Г–≥–Њ—Б—В–Є —Й–µ–њ–Ї–∞ —Б—В—А–µ–Љ–Є—В—Б—П –≤–µ—А–љ—Г—В—М—Б—П –≤ –љ–µ–є—В—А–∞–ї—М–љ–Њ–µ –њ–Њ–ї–Њ–ґ–µ–љ–Є–µ, –љ–Њ –Ј–∞ –≤—А–µ–Љ—П —Б–≤–Њ–µ–≥–Њ –і–≤–Є–ґ–µ–љ–Є—П –Є–Ј –Ї—А–∞–є–љ–µ–≥–Њ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П –≤ –љ–µ–є—В—А–∞–ї—М–љ–Њ–µ –Њ–љ–∞ —Г—Б–њ–µ–≤–∞–µ—В –њ—А–Є–Њ–±—А–µ—Б—В–Є –љ–µ–Ї–Њ—В–Њ—А—Г—О —Б–Ї–Њ—А–Њ—Б—В—М—О –Є –Ј–∞ —Б—З—С—В –Є–љ–µ—А—Ж–Є–Є –њ–Њ–њ—А–Њ—Б—В—Г –њ—А–Њ–ї–µ—В–∞–µ—В –љ–µ–є—В—А–∞–ї—М–љ–Њ–µ –њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –Є —Г—Е–Њ–і–Є—В —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –і–∞–ї—М—И–µ –љ–µ–≥–Њ, –Њ–Ї–∞–Ј—Л–≤–∞—П—Б—М –љ–∞ –Љ–Њ–Љ–µ–љ—В –њ–Њ–≥–∞—И–µ–љ–Є—П —Б–Ї–Њ—А–Њ—Б—В–Є –≤ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–µ–љ–љ–Њ–Љ –Ї—А–∞–є–љ–µ–є –њ–Њ–ї–Њ–ґ–µ–љ–Є–Є. –¶–Є–Ї–ї –Љ–љ–Њ–≥–Њ–Ї—А–∞—В–љ–Њ –њ–Њ–≤—В–Њ—А—П–µ—В—Б—П –Є –Њ—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В—Б—П —В–Њ–ї—М–Ї–Њ –Ј –∞—Б—З—С—В –њ–Њ—В–µ—А—М —Н–љ–µ—А–≥–Є–Є –љ–∞ –і–µ—Д–Њ—А–Љ–∞—Ж–Є—О –Є —А–∞—Б—Б–µ—П–љ–Є–µ –µ—С –≤ –Њ–Ї—А—Г–ґ–∞—О—Й—Г—О —Б—А–µ–і—Г. –Ґ–Є–њ–Є—З–љ—Л–є –Љ–∞—П—В–љ–Є–Ї.
–£ –Є–≥—А–∞—О—Й–µ–≥–Њ –љ–∞ —Й–µ–њ–Ї–µ –љ–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є –Љ–µ–љ—П—В—М —В–Њ–љ –њ–Њ–ї—Г—З–∞–µ–Љ–Њ–≥–Њ –Ј–≤—Г–Ї–∞, –∞ –µ—Б—В—М —В–Њ–ї—М–Ї–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –Љ–µ–љ—П—В—М –∞–Љ–њ–ї–Є—В—Г–і—Г –Ї–Њ–ї–µ–±–∞–љ–Є–є (—В.–µ. –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М –њ–Њ–ї—Г—З–∞–µ–Љ–Њ–≥–Њ –Ј–≤—Г–Ї–∞), –≤–∞—А—М–Є—А—Г—П –≤–µ–ї–Є—З–Є–љ—Г –Є–Ј–љ–∞—З–∞–ї—М–љ–Њ–≥–Њ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П —Й–µ–њ–Ї–Є –Њ—В –љ–µ–є—В—А–∞–ї—М–љ–Њ–≥–Њ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П.
–І–∞—Б—В–Њ—В–∞, —Б –Ї–Њ—В–Њ—А–Њ–є —Й–µ–њ–Ї–∞ —Б–Њ–≤–µ—А—И–∞–µ—В –љ–∞—З–Є–љ–∞–µ—В —Б–Њ–≤–µ—А—И–∞—В—М –Ї–Њ–ї–µ–±–∞–љ–Є—П –њ–Њ—Б–ї–µ –Њ—В–њ—Г—Б–Ї–∞–љ–Є—П –Є–Ј –Ї—А–∞–є–љ–µ–≥–Њ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П, –Ј–∞–≤–Є—Б–Є—В –Њ—В —Г–њ—А—Г–≥–Њ—Б—В–Є –Љ–∞—В–µ—А–Є–∞–ї–∞ —Й–µ–њ–Ї–Є, –Љ–∞—Б—Б—Л —Й–µ–њ–Ї–Є (–Ј–∞–≤–Є—Б—П—Й–µ–є –Њ—В –≥–µ–Њ–Љ–µ—В—А–Є–Є —Й–µ–њ–Ї–Є) –Є –≤ –Љ–∞–ї–Њ–є —Б—В–µ–њ–µ–љ–Є вАФ –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Њ–Ї—А—Г–ґ–∞—О—Й–µ–є —Б—А–µ–і—Л. –Э–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ —Г –Є–≥—А–∞—О—Й–µ–≥–Њ –≤—Б—С –ґ–µ –µ—Б—В—М –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –Љ–µ–љ—П—В—М –і–ї–Є–љ—Г –Ї–Њ–ї–µ–±–ї—О—Й–µ–є—Б—П —З–∞—Б—В–Є —Й–µ–њ–Ї–Є –Є —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –Є–Ј–Љ–µ–љ—П—В—М –Љ–∞—Б—Б—Г –Ї–Њ–ї–µ–±–ї—О—Й–µ–є—Б—П —З–∞—Б—В–Є –Є, –≤ —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –Љ–µ–љ—П—В—М —З–∞—Б—В–Њ—В—Г –Ї–Њ–ї–µ–±–∞–љ–Є–є –Є –њ—А–Њ–Є–Ј–≤–Њ–і–Є–Љ—Л–є —В–Њ–љ, –љ–Њ —Н—В–Њ —В–µ—Е–љ–Є—З–µ—Б–Ї–Є —Б–ї–Њ–ґ–љ–Њ, –њ–Њ—Н—В–Њ–Љ—Г —Н—В–Њ—В –∞—Б–њ–µ–Ї—В –Љ—Л –љ–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ.
–І–∞—Б—В–Њ—В–∞ —В–∞–Ї–Є—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –ї–µ–≥–Ї–Њ –≤—Л—З–Є—Б–ї–µ–љ–∞, –Є –і–Њ–њ—Г—Б—В–Є–Љ, –Љ—Л –µ—С –љ–∞–Ј–Њ–≤—С–Љ
f0.
–Ю–і–љ–∞–Ї–Њ, –Ї–ї—О—З–µ–≤–Њ–є —Д–∞–Ї—В –љ–Њ–Љ–µ—А 1 —Б–Њ—Б—В–Њ–Є—В –≤ —В–Њ–Љ, —З—В–Њ –≤ —Б–Є–ї—Г —П–≤–ї–µ–љ–Є—П —А–µ–Ј–Њ–љ–∞–љ—Б–∞, –≤ —Й–µ–њ–Ї–µ –≤–Њ–Ј–љ–Є–Ї–∞—О—В –љ–µ —В–Њ–ї—М–Ї–Њ –Ї–Њ–ї–µ–±–∞–љ–Є—П —Б —З–∞—Б—В–Њ—В–Њ–є
fr, –љ–Њ –Є –Ї–Њ–ї–µ–±–∞–љ–Є—П –љ–∞ —З–∞—Б—В–Њ—В–∞—Е, –Ї—А–∞—В–љ—Л—Е
fr.
–Ш –њ–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ –Ї–Њ–ї–µ–±–∞–љ–Є—П —Й–µ–њ–Ї–Є —Б–Њ—Б—В–∞–≤–ї—П—О—В —Б—Г–њ–µ—А–њ–Њ–Ј–Є—Ж–Є—О –Ї–Њ–ї–µ–±–∞–љ–Є–є –љ–∞ —З–∞—Б—В–Њ—В–∞—Е
f0, 2
¬Јf0, 3¬Ј
f0, 4¬Ј
f0, ... k¬Ј
f0–°–Є–љ—Г—Б–Њ–Є–і–∞–ї—М–љ—Л–µ –Ї–Њ–ї–µ–±–∞–љ–Є—П –љ–∞ —З–∞—Б—В–Њ—В–µ
f0 –љ–∞–Ј—Л–≤–∞—О—В—Б—П
–Њ—Б–љ–Њ–≤–љ—Л–Љ —В–Њ–љ–Њ–Љ, –∞ –Ї–Њ–ї–µ–±–∞–љ–Є—П –љ–∞ –±–Њ–ї–µ–µ –≤—Л—Б–Њ–Ї–Є—Е –Ї—А–∞—В–љ—Л—Е —З–∞—Б—В–Њ—В–∞—Е вАФ
–Њ–±–µ—А—В–Њ–љ–∞–Љ–Є. –°–Њ–±—Б—В–≤–µ–љ–љ–Њ, ¬Ђ–Њ–±–µ—А¬ї вАФ —Н—В–Њ –љ–µ–Љ–µ—Ж–Ї–Њ–µ ¬Ђ–љ–∞–і¬ї, —В–Њ—З–љ–Њ —В–∞–Ї–Њ–µ –ґ–µ, –Ї–∞–Ї –∞–љ–≥–ї–Є–є—Б–Ї–Њ–µ
over.
(–°—Г—Й–µ—Б—В–≤—Г–µ—В —В–∞–Ї –ґ–µ —В–µ—А–Љ–Є–љ, —Г–љ—В–µ—А—В–Њ–љ—Л вАФ¬†—Б–Љ—Л—Б–ї —Б–ї–Њ–≤–∞, —П –і—Г–Љ–∞—О, –њ–Њ–љ—П—В–µ–љ –њ–Њ –∞–љ–∞–ї–Њ–≥–Є–Є)–Ш–Љ–µ–љ–љ–Њ –љ–∞–ї–Є—З–Є–µ –Њ–±–µ—А—В–Њ–љ–Њ–≤ –і–∞—С—В —Й–µ–њ–Ї–µ —Е–∞—А–∞–Ї—В–µ—А–љ–Њ–µ –Ј–≤—Г—З–∞–љ–Є–µ; –Є–Љ–µ–љ–љ–Њ –≤ —Б–Є–ї—Г –љ–∞–ї–Є—З–Є—П –Њ–±–µ—А—В–Њ–љ–Њ–≤ —Й–µ–њ–Ї–∞ –љ–µ –Ј–≤—Г—З–Є—В –Ї–∞–Ї –Њ–і–Є–љ–Њ—З–љ—Л–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞–ї—М–љ—Л–µ –Ї–Њ–ї–µ–±–∞–љ–Є—П –љ–∞ –Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ–є —З–∞—Б—В–Њ—В–µ.
–Ґ–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є, –Ї–Њ–≥–і–∞ –Ј–≤—Г—З–Є—В —Й–µ–њ–Ї–∞, —А—П–і –њ–Њ–ї—Г—З–∞–µ–Љ—Л—Е –Њ–±–µ—А—В–Њ–љ–Њ–≤ вАФ¬†–±–µ—Б–Ї–Њ–љ–µ—З–µ–љ. –Э–∞ –њ—А–∞–Ї—В–Є–Ї–µ –ґ–µ –∞–±—Б–Њ–ї—О—В–љ–Њ –≤—Б–µ –Ї–Њ–ї–µ–±–∞–љ–Є—П (–Є –Њ—Б–љ–Њ–≤–љ–Њ–є —В–Њ–љ –Є –Њ–±–µ—А—В–Њ–љ—Л) –Ј–∞—В—Г—Е–∞—О—В, –њ—А–Є—З—С–Љ –і–ї—П —З–µ–Љ –≤—Л—И–µ —З–∞—Б—В–Њ—В–∞ –Ї–Њ–ї–µ–±–∞–љ–Є–є вАФ —В–µ–Љ –±—Л—Б—В—А–µ–µ –Њ–љ–Є –Ј–∞—В—Г—Е–∞—О—В. –Я–Њ—Н—В–Њ–Љ—Г –љ–∞ –њ—А–∞–Ї—В–Є–Ї–µ —А—П–і –Њ–±–µ—А—В–Њ–љ–Њ–≤ –Љ–Њ–ґ–љ–Њ —Б—З–Є—В–∞—В—М –Њ–≥—А–∞–љ–Є—З–µ–љ–љ—Л–Љ —Б–≤–µ—А—Е—Г вАФ —Б–ї–Є—И–Ї–Њ–Љ –≤—Л—Б–Њ–Ї–Њ—З–∞—Б—В–Њ—В–љ—Л–µ –Њ–±–µ—А—В–Њ–љ—Л –Ј–∞—В—Г—Е–∞—О—В –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –Љ–≥–љ–Њ–≤–µ–љ–љ–Њ, –њ–Њ –Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ, –і–Њ —Г—А–Њ–≤–љ—П, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ —Г—Е–Њ (–і–∞ –Є –і—А—Г–≥–Є–µ –Ј–≤—Г–Ї–Њ—Д–Є–Ї—Б–Є—А—Г—О—Й–Є–µ —Г—Б—В—А–Њ–є—Б—В–≤–∞) –љ–µ –Љ–Њ–≥—Г—В –Є—Е –Ј–∞—Д–Є–Ї—Б–Є—А–Њ–≤–∞—В—М, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –Є—Е –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М –≤ –љ–∞ –Љ–љ–Њ–≥–Њ –њ–Њ—А—П–і–Ї–Њ–≤ –љ–Є–ґ–µ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є —В–Њ–≥–Њ –ґ–µ –Њ—Б–љ–Њ–≤–љ–Њ–≥–Њ —В–Њ–љ–∞.
–°–њ–µ–Ї—В—А –Ј–≤—Г–Ї–∞, –Є–Ј–і–∞–≤–∞–µ–Љ–Њ–≥–Њ –≤–Є–±—А–Є—А—Г—О—Й–µ–є —Й–µ–њ–Ї–Њ–є –≤ –љ–∞—З–∞–ї—М–љ—Л–є –Љ–Њ–Љ–µ–љ—В –µ—С –Ј–≤—Г—З–∞–љ–Є—П:
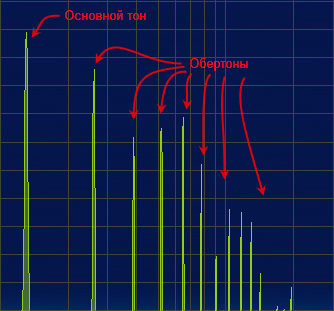
–У–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–∞—П –Њ—Б—М вАФ¬†—З–∞—Б—В–Њ—В—Л, –≤–µ—А—В–Є–Ї–∞–ї—М–љ–∞—П вАФ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є. –®–Ї–∞–ї–∞ –њ–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї–Є вАФ –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–∞—П. –¶–µ–љ–∞ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Њ–≥–Њ –і–µ–ї–µ–љ–Є—П вАФ —Б–љ–∞—З–∞–ї–∞ 100 –У—Ж, –Ј–∞—В–µ–Љ 1000 –У—Ж.
–Т–Њ–Њ–±—Й–µ, –і–ї—П –ї—О–±—Л—Е –Є–љ—Б—В—А—Г–Љ–µ–љ—В–Њ–≤ —Б–њ–µ–Ї—В—А–∞–ї—М–љ—Л–є —Б–Њ—Б—В–∞–≤ –Ј–≤—Г–Ї–∞ –Є —Е–∞—А–∞–Ї—В–µ—А –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Ї–∞–ґ–і–Њ–є —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–є —Б–Њ—Б—В–∞–≤–ї—П—О—Й–µ–є –њ–Њ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є (–∞ –Є–љ–Њ–≥–і–∞ –Є —З–∞—Б—В–Њ—В–µ) –≤–Њ –≤—А–µ–Љ–µ–љ–Є вАФ –Њ–њ—А–µ–і–µ–ї—П–µ—В —Г–љ–Є–Ї–∞–ї—М–љ—Л–є —В–µ–Љ–±—А —Н—В–Њ–≥–Њ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞.
–≠—В–Њ –ґ–µ –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї —В–∞–Ї–Њ–Љ—Г –Є–љ—Б—В—А—Г–Љ–µ–љ—В—Г –Ї–∞–Ї —З–µ–ї–Њ–≤–µ—З–µ—Б–Ї–Є–є –≥–Њ–ї–Њ—Б. –°–њ–µ–Ї—В—А–Њ–≥—А–∞–Љ–Љ–∞ —З–µ–ї–Њ–≤–µ—З–µ—Б–Ї–Њ–≥–Њ –≥–Њ–ї–Њ—Б–∞:
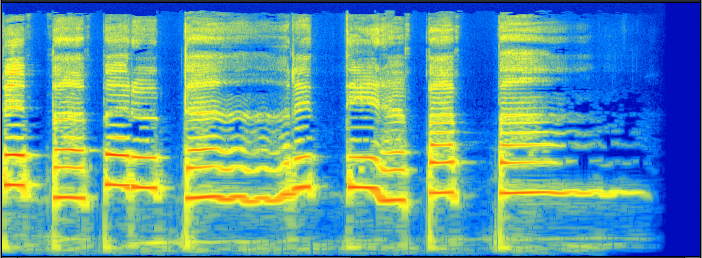
–У–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–∞—П –Њ—Б—М вАФ –≤—А–µ–Љ—П, –ї–Є–љ–µ–є–љ—Л–є –Љ–∞—Б—И—В–∞–±. –Т–µ—А—В–Є–Ї–∞–ї—М–љ–∞—П –Њ—Б—М вАФ —З–∞—Б—В–Њ—В–∞, –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Є–є –Љ–∞—Б—И—В–∞–±.
–Т—Б—С –≤—Л—И–µ—Б–Ї–∞–Ј–∞–љ–љ–Њ–µ –Њ–± –Њ—Б–љ–Њ–≤–љ–Њ–Љ —В–Њ–љ–µ –Є –Њ–±–µ—А—В–Њ–љ–∞—Е, –Ї–∞–Ї –≤–Є–і–љ–Њ, –≤ —В–Њ–є –ґ–µ —Б—В–µ–њ–µ–љ–Є –Њ—В–љ–Њ—Б–Є—В—Б—П –Є –Ї –≥–Њ–ї–Њ—Б—Г, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≥–Њ–ї–Њ—Б–Њ–≤–∞—П —Й–µ–ї—М –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —В–∞–Ї—Г—О –ґ–µ —А–µ–Ј–Њ–љ–Є—А—Г—О—Й—Г—О —Б–Є—Б—В–µ–Љ—Г, –Ї–∞–Ї –Є —Й–µ–њ–Ї–∞ –љ–∞ –њ–љ–µ, –Є –≤ —Ж–µ–ї–Њ–Љ –≥–Њ–ї–Њ—Б–Њ–≤—Л–µ —Б–Ї–ї–∞–і–Ї–Є –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л —Б—В—А—Г–љ–∞–Љ: —З–µ–ї–Њ–≤–µ–Ї —А–µ–≥—Г–ї–Є—А—Г–µ—В –≤—Л—Б–Њ—В—Г —В–Њ–љ–∞ –Є–Ј–Љ–µ–љ—П—П —Б–Є–ї—Г –љ–∞—В—П–ґ–µ–љ–Є—П
—Б—В—А—Г–љ—Л —Б–Ї–ї–∞–і–Њ–Ї. –Э–∞ —Б–њ–µ–Ї—В—А–Њ–≥—А–∞–Љ–Љ–µ –≤–Є–і–љ–Њ, —З—В–Њ –љ–∞–Є–±–Њ–ї–µ–µ —Б–Є–ї—М–љ–Њ –њ—А–Њ—П–≤–ї—П—О—В—Б—П –Њ—Б–љ–Њ–≤–љ–Њ–є —В–Њ–љ –Є –њ–µ—А–≤—Л–є –Њ–±–µ—А—В–Њ–љ, –Њ—В—Б—В–Њ—П—Й–Є–µ –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞ –љ–∞ –Њ–і–љ—Г –Њ–Ї—В–∞–≤—Г.
–Ш—В–∞–Ї, –µ—Б–ї–Є —Г –≤–∞—Б –µ—Б—В—М –њ–µ–љ—М —Б —Й–µ–њ–Ї–Њ–є, –≤—Л –Љ–Њ–ґ–µ—В–µ —Б—Л–≥—А–∞—В—М –љ–∞ –љ—С–Љ –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л–є
—А–Є—В–Љ, –љ–Њ –≤—Л –љ–µ –Љ–Њ–ґ–µ—В–µ —Б—Л–≥—А–∞—В—М –Ї–∞–Ї—Г—О-–ї–Є–±–Њ –Љ–µ–ї–Њ–і–Є—О, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –њ–µ–љ—М —Б —Й–µ–њ–Ї–Њ–є –≤—Б—С –≤—А–µ–Љ—П –Є–Ј–і–∞—С—В —В–Њ–љ –Њ–і–љ–Њ–є –Є —В–Њ–є –ґ–µ –≤—Л—Б–Њ—В—Л (—З–∞—Б—В–Њ—В–∞ –Њ—Б–љ–Њ–≤–љ–Њ–≥–Њ —В–Њ–љ–∞, –∞ –Ј–љ–∞—З–Є—В –Є —З–∞—Б—В–Њ—В—Л –≤—Б–µ—Е –Њ–±–µ—А—В–Њ–љ–Њ–≤, –≤—Б–µ –≤—А–µ–Љ—П –Њ–і–љ–Є –Є —В–µ –ґ–µ). –° —Г—З—С—В–Њ–Љ —В–Њ–≥–Њ, —З—В–Њ —З–µ–ї–Њ–≤–µ—З–µ—Б–Ї–Є–є –≥–Њ–ї–Њ—Б –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Љ–µ–љ—П—В—М –≤—Л—Б–Њ—В—Г —В–Њ–љ–∞ –Є –Є–Ј–і–∞–≤–∞—В—М –ї—О–±—Л–µ —В–Њ–љ–∞ –Є–Ј –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –і–Є–∞–њ–∞–Ј–Њ–љ–∞, –њ–Њ–љ—П—В–љ–Њ, —З—В–Њ —З–µ–ї–Њ–≤–µ–Ї—Г —Е–Њ—В–µ–ї–Њ—Б—М –Є–Љ–µ—В—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В, —Б–њ–Њ—Б–Њ–±–љ—Л–є –Є–Ј–і–∞–≤–∞—В—М –±–Њ–ї–µ–µ —З–µ–Љ –Њ–і–љ—Г –љ–Њ—В—Г. –Я–Њ—Н—В–Њ–Љ—Г —В–∞–Ї–Є–µ –Є–љ—Б—В—А—Г–Љ–µ–љ—В—Л –±—Л–ї–Є —Б–Њ–Ј–і–∞–љ—Л.
–Э–µ –≤–∞–ґ–љ–Њ, –Ї–∞–Ї–Є–Љ –Є–љ—В–µ—А—Д–µ–є—Б–Њ–Љ –Њ–±–ї–∞–і–∞–µ—В –Є–љ—В–µ—А—Д–µ–є—Б: –Ї–ї–∞–≤–Є—И–Є –ї–Є, –Є–ї–Є —Б—В—А—Г–љ—Л, –Є–ї–Є –њ–ї–Њ—Й–∞–і–Ї–Є, –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г –љ—Г–ґ–љ–Њ —Г–і–∞—А—П—В—М –Љ–Њ–ї–Њ—В–Њ—З–Ї–Њ–Љ, –Є–ї–Є —В—А—Г–±–Ї–Є, –≤ –Ї–Њ—В–Њ—А—Л–µ –љ—Г–ґ–љ–Њ –і—Г—В—М вАФ –Є–Ј –љ–∞–±–Њ—А–∞ –Ј–≤—Г–Ї–Њ–≤ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е —З–∞—Б—В–Њ—В –Љ—Г–Ј—Л–Ї–∞ –Ї–∞–Ї-—В–Њ –љ–µ –њ–Њ–ї—Г—З–∞–ї–∞—Б—М, –њ–Њ—Н—В–Њ–Љ—Г —Б—В–∞–ї–∞ –њ–Њ–љ—П—В–љ–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М –љ–∞–ї–Є—З–Є—П –і–Є—Б–Ї—А–µ—В–љ–Њ–≥–Њ –љ–∞–±–Њ—А–∞ –Ј–≤—Г–Ї–Њ–≤ –Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ–є –≤—Л—Б–Њ—В—Л вАФ –љ–Њ—В.
–Ю—Б–Њ–±–∞—П –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј—М —А—П–і–∞ –Ј–≤—Г–Ї–Њ–≤, –Њ—В—Б—В–Њ—П—Й–Є—Е –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞ –њ–Њ –≤—Л—Б–Њ—В–µ (–њ–Њ —З–∞—Б—В–Њ—В–µ) –љ–∞ –Є–љ—В–µ—А–≤–∞–ї –≤ –Њ–і–љ—Г –Њ–Ї—В–∞–≤—Г, –±—Л–ї–∞ –Є–Ј–≤–µ—Б—В–µ–љ –і–∞–≤–љ–Њ, –Њ–і–љ–∞–Ї–Њ –ґ–µ –µ—Б–ї–Є –≤ –Ї–∞—З–µ—Б—В–≤–µ –љ–Њ—В –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —Н—В–Њ—В —А—П–і –Ј–≤—Г–Ї–Њ–≤, —В–Њ –љ–Є—З–µ–≥–Њ –Є–љ—В–µ—А–µ—Б–љ–Њ–≥–Њ –Є–Ј —Н—В–Њ–≥–Њ –љ–µ –њ–Њ–ї—Г—З–Є—В—Б—П: –Є–љ—В–µ—А–≤–∞–ї –≤ –Њ–і–љ—Г –Њ–Ї—В–∞–≤—Г —Б–ї–Є—И–Ї–Њ–Љ –≤–µ–ї–Є–Ї, –љ–Њ —З—В–Њ –µ—Й—С —Е—Г–ґ–µ, –≤—Б–µ –љ–Њ—В—Л, —В–Њ–љ –Ї–Њ—В–Њ—А—Л—Е –Њ—В—Б—В–Њ–Є—В –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞ –љ–∞ –Њ–і–љ—Г –Њ–Ї—В–∞–≤—Г, –Њ–±–ї–∞–і–∞—О—В –Њ—З–µ–љ—М —Е–Њ—А–Њ—И–Њ –Њ—Й—Г—Й–∞–µ–Љ—Л–Љ –Ј–≤—Г–Ї–Њ–≤—Л–Љ —Б—А–Њ–і—Б—В–≤–Њ–Љ –Є –≤–Њ—Б–њ—А–Є–љ–Є–Љ–∞—О—В—Б—П –Ї–∞–Ї ¬Ђ–Њ–і–љ–∞ –Є —В–∞ –ґ–µ –њ–Њ —Б—Г—В–Є¬ї –љ–Њ—В–∞ –љ–Њ —Б —А–∞–Ј–љ–Њ–є –≤—Л—Б–Њ—В–Њ–є –Ј–≤—Г—З–∞–љ–Є—П. –Я—А–Є—З—С–Љ, —З–µ–Љ –±–Њ–≥–∞—З–µ –Њ–±–µ—А—В–Њ–љ–Њ–≤—Л–є —Б–Њ—Б—В–∞–≤ —В–∞–Ї–Є—Е –љ–Њ—В (–Є —З–µ–Љ –Љ–µ–љ—М—И–µ–є –Є –±–Њ–ї–µ–µ –≥–ї–∞–і–Ї–Њ–є —А–∞–Ј–љ–Є—Ж–∞ –Љ–µ–ґ–і—Г –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М—О –Њ–±–µ—А—В–Њ–љ–Њ–≤), —В–µ–Љ –Љ–µ–љ–µ–µ –≤—Л—А–∞–ґ–µ–љ–љ–Њ–є —Б—В–∞–љ–Њ–≤–Є—В—Б—П —А–∞–Ј–љ–Є—Ж–∞ –Љ–µ–ґ–і—Г —В–∞–Ї–Є–Љ–Є –љ–Њ—В–∞–Љ–Є.
–Я–Њ—Н—В–Њ–Љ—Г –≤–Ј—П—В—М –≤ –Ї–∞—З–µ—Б—В–≤–µ –љ–Њ—В –Ј–≤—Г–Ї–Є, —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–љ—Л–µ –њ–Њ —Б–µ—В–Ї–µ —З–∞—Б—В–Њ—В —Б —И–∞–≥–Њ–Љ –≤ –Њ–Ї—В–∞–≤—Г вАФ –љ–µ –њ–Њ–і—Е–Њ–і–Є—В. –Ъ–Њ–љ–µ—З–љ–Њ, –Ї–∞–Ї—Г—О-—В–Њ –Љ—Г–Ј—Л–Ї—Г —Б –±–Њ–ї—М—И–Њ–є –љ–∞—В—П–ґ–Ї–Њ–є –љ–∞ —В–∞–Ї–Њ–µ –Ј–≤–∞–љ–Є–µ –Є –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ –±—Л —Б–Њ—З–Є–љ–Є—В—М –Є –Є—Б–њ–Њ–ї–љ–Є—В—М, –љ–Њ...
–Х—Б—В–µ—Б—В–≤–µ–љ–љ–Њ –≤–Њ–Ј–љ–Є–Ї–∞—О—Й–∞—П –Љ—Л—Б–ї—М: —А–∞–Ј–±–Є—В—М –Њ–Ї—В–∞–≤–љ—Г—О —Б–µ—В–Ї—Г –љ–∞ –±–Њ–ї–µ–µ –Љ–µ–ї–Ї–Є–µ –Є–љ—В–µ—А–≤–∞–ї—Л –Є –≤–Ј—П—В—М –њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ—Л–µ —В–Њ—З–Ї–Є –≤ –Ї–∞—З–µ—Б—В–≤–µ –љ–Њ—В. –° —Г—З—С—В–Њ–Љ —В–Њ–≥–Њ, —З—В–Њ —З–µ–ї–Њ–≤–µ—З–µ—Б—В–≤–Њ –ї–µ–≥–Ї–Њ —Г—Б—В–∞–љ–Њ–≤–Є–ї–Њ —Б–≤—П–Ј—М —В–Њ–љ–∞ –Є –і–ї–Є–љ—Г/–љ–∞—В—П–ґ—С–љ–љ–Њ—Б—В–Є —Б—В—А—Г–љ—Л, —Н—В–Њ –љ–µ –±—Л–ї–Њ –±–Њ–ї—М—И–Њ–є –њ—А–Њ–±–ї–µ–Љ–Њ–є, –Є –Љ–µ–љ—П—П –Ї–∞–Ї–Њ–є-–ї–Є–±–Њ –њ–∞—А–∞–Љ–µ—В—А (–і–ї–Є–љ—Г/–љ–∞—В—П–ґ—С–љ–љ–Њ—Б—В—М) –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ –њ–Њ–ї—Г—З–∞—В—М —В–Њ–љ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–є –≤—Л—Б–Њ—В—Л.
–Ю–і–љ–∞–Ї–Њ —В—Г—В –≤–Њ–Ј–љ–Є–Ї–∞—О—В
—В—А–Є –≥–ї–∞–≤–љ—Л—Е –≤–Њ–њ—А–Њ—Б–∞, –Ї–Њ—В–Њ—А—Л–µ –ї–µ–ґ–∞—В –≤ –Њ—Б–љ–Њ–≤–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В–Є –≤–≤–Њ–і–∞ –Ї–Њ–љ–≤–µ–љ—Ж–Є–є:
- –Э–∞ —Б–Ї–Њ–ї—М–Ї–Њ –±–Њ–ї–µ–µ –Љ–µ–ї–Ї–Є—Е –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ –і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г? –Ф–≤–∞? –Ґ—А–Є? –Я—П—В—М? –Ф–µ—Б—П—В—М? –Ф–≤–∞–і—Ж–∞—В—М?
- –Я–Њ –Ї–∞–Ї–Њ–Љ—Г –њ—А–Є–љ—Ж–Є–њ—Г –і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г? –Ф–Њ–ї–ґ–љ—Л –ї–Є –Є–љ—В–µ—А–≤–∞–ї—Л –±—Л—В—М —А–∞–≤–љ—Л–Љ–Є? –Ф–Њ–ї–ґ–љ—Л –ї–Є –Њ–љ–Є –±—Л—В—М —А–∞–≤–љ—Л–Љ–Є –≤ –∞–±—Б–Њ–ї—О—В–љ–Њ–Љ –Є–ї–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–Є?
- –Ю—В –Ї–∞–Ї–Њ–є —З–∞—Б—В–Њ—В—Л —Б—В—А–Њ–Є—В—М –Њ–Ї—В–∞–≤–љ—Г—О —Б–µ—В–Ї—Г?
–Я–Њ —Б—Г—В–Є, –µ—Б–ї–Є –њ—А–µ–і—Б—В–∞–≤–Є—В—М, —З—В–Њ –љ–∞–Љ –Є–Ј–≤–µ—Б—В–µ–љ —В–Њ–ї—М–Ї–Њ —В–Њ—В —Д–∞–Ї—В, —З—В–Њ –Є–љ—В–µ—А–≤–∞–ї –≤ –Њ–Ї—В–∞–≤—Г –Њ–±–ї–∞–і–∞–µ—В —Г–љ–Є–Ї–∞–ї—М–љ—Л–Љ–Є —Б–≤–Њ–є—Б—В–≤–∞–Љ–Є (–≤ –њ–µ—А–≤—Г—О –Њ—З–µ—А–µ–і—М —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –≤–Њ—Б–њ—А–Є—П—В–Є—П) –Є —З—В–Њ –Њ–љ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –њ—А–µ–≤–Њ—Б—Е–Њ–і—Б—В–≤—Г —З–∞—Б—В–Њ—В—Л –≤–і–≤–Њ–µ, —Г –љ–∞—Б –µ—Б—В—М —В–Њ–ї—М–Ї–Њ —Б–ї–µ–і—Г—О—Й–∞—П –Ї–∞—А—В–Є–љ–∞:
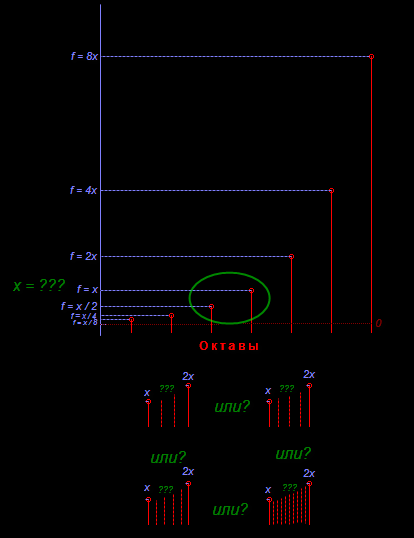
–Э–µ–њ–Њ–љ—П—В–љ–Њ, —З–µ–Љ—Г –і–Њ–ї–ґ–µ–љ –±—Л—В—М —А–∞–≤–µ–љ
x, –љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ –Ї—Г—Б–Њ—З–Ї–Њ–≤ –і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г —З—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М –њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ—Л–µ –љ–Њ—В—Л –Є, —З—В–Њ –µ—Й—С –≤–∞–ґ–љ–µ–µ, –і–∞–ґ–µ –µ—Б–ї–Є –±—Г–і–µ—В –Њ–њ—А–µ–і–µ–ї–µ–љ–Њ —Н—В–Њ —З–Є—Б–ї–Њ, –Ї–∞–Ї –≤—Л—З–Є—Б–ї–Є—В—М —З–∞—Б—В–Њ—В—Г –Ї–Њ–љ–Ї—А–µ—В–љ–Њ–є –њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ–Њ–є —В–Њ—З–Ї–Є (–Є –≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ –µ–є –њ–Њ–і–Њ–±—А–∞—В—М –і–ї–Є–љ—Г –Є–ї–Є —Б–Є–ї—Г –љ–∞—В—П–ґ–µ–љ–Є—П —Б—В—А—Г–љ—Л, –Ї –њ—А–Є–Љ–µ—А—Г)?
–Я–Њ–њ—Л—В–Ї–Є —А–µ—И–Є—В—М —Н—В—Г –њ—А–Њ–±–ї–µ–Љ—Г –њ—А–µ–і–њ—А–Є–љ–Є–Љ–∞–ї–Є—Б—М –Њ—З–µ–љ—М –і–∞–≤–љ–Њ, –Ї–∞–Ї –Љ–Є–љ–Є–Љ—Г–Љ –µ—Й—С –і–Њ –љ–∞—И–µ–є —Н—А—Л, –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —З–µ–≥–Њ –±—Л–ї –њ—А–Є–љ—П—В
–Я–Є—Д–∞–≥–Њ—А–Њ–≤ —Б—В—А–Њ–є.
–Т–Њ–Њ–±—Й–µ,
—Б—В—А–Њ–є вАФ —Н—В–Њ –Є –µ—Б—В—М –Ї–Њ–љ—Ж–µ–њ—Ж–Є—П —В–Њ–≥–Њ –Є–ї–Є —Б–Њ–≥–ї–∞—И–µ–љ–Є–µ –Њ —В–Њ–Љ, –Ї–∞–Ї –Є –љ–∞ –Ї–∞–Ї–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ –і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г, —З—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М ¬Ђ–њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ—Л–µ¬ї –љ–Њ—В—Л. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г —В–∞–Ї–Є–µ –≤–µ—Й–Є, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –Є –ї–Њ–≥–∞—А–Є—Д–Љ –љ–µ –±—Л–ї–Є –Є–Ј–≤–µ—Б—В–љ—Л –ї—О–і—П–Љ –≤ –і—А–µ–≤–љ–Њ—Б—В–Є, –њ–Њ–њ—Л—В–Ї–Є –њ–Њ–і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г –њ—А–µ–і–њ—А–Є–љ–Є–Љ–∞–ї–Є—Б—М –љ–∞ –Њ—Б–љ–Њ–≤–µ –і—А–Њ–±–ї–µ–љ–Є—П –µ—С –љ–∞ —В–∞–Ї–Є–µ –Є–љ—В–µ—А–≤–∞–ї—Л, —З—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г —З–∞—Б—В–Њ—В–∞–Љ–Є —Б–Њ—Б–µ–і–љ–Є—Е –љ–Њ—В –Њ–њ–Є—Б—Л–≤–∞–ї–Њ—Б—М –±—Л —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ –љ–∞—В—Г—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї.
–°—В—А–Њ–µ–≤ –±—Л–ї–Њ —Б–Њ–Ј–і–∞–љ–Њ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ:
–Я—А–Є—З–Є–љ–∞, –њ–Њ –Ї–Њ—В–Њ—А–Њ–є –±—Л–ї–Є —Б–Њ–Ј–і–∞–љ—Л —А–∞–Ј–љ—Л–µ —Б—В—А–Њ–Є, –≤ —В–Њ–Љ, —З—В–Њ –љ–Є –Њ–і–Є–љ –Є–Ј –≤–∞—А–Є–∞–љ—В–Њ–≤ —А–µ—И–µ–љ–Є—П –њ—А–Њ–±–ї–µ–Љ—Л –љ–µ –±—Л–ї –∞–±—Б–Њ–ї—О—В–љ–Њ –Є–і–µ–∞–ї—М–љ—Л–Љ. –Я–Њ–њ—Л—В–Ї–Є —А–∞–Ј–і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г –љ–∞ –њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ—Л–µ –љ–Њ—В—Л, –Є—Б–њ–Њ–ї—М–Ј—Г—П –њ–Њ–і—Е–Њ–і, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ —З–∞—Б—В–Њ—В—Л –љ–Њ—В –≤—Л—З–Є—Б–ї—П–ї–Є—Б—М —З–µ—А–µ–Ј —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П –љ–∞—В—Г—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї, –і–∞–≤–∞–ї–Є —В–∞–Ї—Г—О —Б–µ—В–Ї—Г —З–∞—Б—В–Њ—В, —З—В–Њ –љ–µ–Ї–Њ—В–Њ—А—Л–µ –Є–љ—В–µ—А–≤–∞–ї—Л –Ј–≤—Г—З–∞–ї–Є –Њ—В–Ї—А–Њ–≤–µ–љ–љ–Њ –њ–ї–Њ—Е–Њ (—В.–љ. ¬Ђ—Д–∞–ї—М—И–Є–≤–Њ¬ї).
–Ґ–∞–Ї, –љ–∞–њ—А–Є–Љ–µ—А, —Б –љ–µ–Ї–Њ—В–Њ—А—Л–Љ —Г–њ—А–Њ—Й–µ–љ–Є–µ–Љ –Є–Ј–ї–Њ–ґ–µ–љ–Є—П, –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М, —З—В–Њ –љ–∞—В—Г—А–∞–ї—М–љ—Л–є —Б—В—А–Њ–є –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–ї —А–∞–Ј–і–µ–ї–µ–љ–Є–µ –Њ–Ї—В–∞–≤—Л –љ–∞ 12 –њ—А–Є–Љ–µ—А–љ–Њ —А–∞–≤–љ—Л—Е (–љ–∞ —Б–ї—Г—Е) –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ —Б –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ–Љ —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤ –Ї–∞–ґ–і–Њ–є –Њ–Ї—В–∞–≤–µ 12 –љ–Њ—В.
–Ш–љ—В–µ—А–≤–∞–ї—Л –Љ–µ–ґ–і—Г —Б–Њ—Б–µ–і–љ–Є–Љ–Є –љ–Њ—В–∞–Љ–Є –љ–µ –±—Л–ї–Є –∞–±—Б–Њ–ї—О—В–љ–Њ –Є–і–µ–љ—В–Є—З–љ—Л–Љ–Є: –њ—А–Њ–њ–Њ—А—Ж–Є—П —З–∞—Б—В–Њ—В –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П —Б–Њ—Б–µ–і–љ–Є–Љ–Є –љ–Њ—В–∞–Љ–Є –Љ–Њ–≥–ї–∞ –±—Л—В—М –ї–Є–±–Њ 15:16, –ї–Є–±–Њ 128:135, –ї–Є–±–Њ 24:25.
–Ґ–µ–Љ –љ–µ –Љ–µ–љ–µ–µ, –±–ї–∞–≥–Њ–і–∞—А—П —А–∞–Ј–≤–Є—В–Є—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –Є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–Љ—Г –њ–Њ–Є—Б–Ї—Г –Є–і–µ–∞–ї—М–љ–Њ–≥–Њ —Б—В—А–Њ—П, —Б–љ–∞—З–∞–ї–∞ –±—Л–ї –њ—А–µ–і–ї–Њ–ґ–µ–љ –Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ —А–∞—Б—Б—З–Є—В–∞–љ, –∞ –њ–Њ—В–Њ–Љ (–љ–∞—З–Є–љ–∞—П —Б 18-–≥–Њ –≤–µ–Ї–∞) –Є –њ–Њ–ї—Г—З–Є–ї —А–Њ–ї—М –≥–Њ—Б–њ–Њ–і—Б—В–≤—Г—О—Й–µ–≥–Њ —Б—В—А–Њ–є, –Ї–Њ—В–Њ—А—Л–є –Љ–Њ–ґ–љ–Њ —Б—З–Є—В–∞—В—М –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Є–і–µ–∞–ї—М–љ—Л–Љ –Є –Ї–Њ—В–Њ—А—Л–є –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –њ–Њ —Б–µ–≥–Њ–і–љ—П—И–љ–Є–є –і–µ–љ—М вАФ
—А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ—Л–є —Б—В—А–Њ–є.
–Ш–і–µ—П –њ—А–Њ—Б—В–∞:
- –Њ–Ї—В–∞–≤–∞ –і–µ–ї–Є—В—Б—П –љ–∞ 12 –Є—Б—В–Є–љ–љ–Њ —А–∞–≤–љ—Л—Е –Ї—Г—Б–Њ—З–Ї–Њ–≤ (–Є–љ—В–µ—А–≤–∞–ї–Њ–≤), —Б –њ–Њ–ї—Г—З–µ–љ–Є–µ–Љ –≤ –Ї–∞–ґ–і–Њ–є –Њ–Ї—В–∞–≤–µ 12 –љ–Њ—В.
- –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ–Ї—В–∞–≤–∞ вАФ —Н—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —З–∞—Б—В–Њ—В 1:2, –∞ –Љ—Л –і–µ–ї–Є–Љ –µ—С –љ–∞ 12 –Є–љ—В–µ—А–≤–∞–ї–Њ–≤, –Ї–∞–ґ–і—Л–є –Є–љ—В–µ—А–≤–∞–ї вАФ —Н—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —З–∞—Б—В–Њ—В 1:21/12
- —З–∞—Б—В–Њ—В–∞ –Ї–∞–ґ–і–Њ–є –њ–Њ—Б–ї–µ–і—Г—О—Й–µ–є –љ–Њ—В—Л –±–Њ–ї—М—И–µ —З–∞—Б—В–Њ—В—Л –њ—А–µ–і—Л–і—Г—Й–µ–є –љ–Њ—В—Л –≤ 21/12 —А–∞–Ј–∞
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –Ї–∞–Ї –Є –љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ –њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ—Л—Е –љ–Њ—В —А–∞–Ј–і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г, –љ–∞ –≤–Њ–њ—А–Њ—Б –Њ —В–Њ–Љ, –Ї–∞–Ї—Г—О —З–∞—Б—В–Њ—В—Г –±—А–∞—В—М –≤ –Ї–∞—З–µ—Б—В–≤–µ –Њ–њ–Њ—А–љ–Њ–є, —З—В–Њ–±—Л –љ–∞ –µ—С –Њ—Б–љ–Њ–≤–µ —А–∞—Б—З–Є—В—Л–≤–∞—В—М —З–∞—Б—В–Њ—В—Л –≤—Б–µ—Е –Њ—Б—В–∞–ї—М–љ—Л—Е –љ–Њ—В, —В–Њ–ґ–µ –±—Л–ї –і–∞–љ –Њ—В–≤–µ—В. –•–Њ—В—П —Н—В–Њ —З–Є—Б–ї–Њ –љ–µ –њ–Њ–і–Ї—А–µ–њ–ї–µ–љ–Њ –љ–Є–Ї–∞–Ї–Њ–є –∞–±—Б–Њ–ї—О—В–љ–Њ–є –Є—Б—В–Є–љ–Њ–є –Є –љ–Є—З–µ–Љ –љ–µ –ї—Г—З—И–µ –Є –љ–µ —Е—Г–ґ–µ –і—А—Г–≥–Є—Е —З–Є—Б–µ–ї, –Ј–∞ –Њ–њ–Њ—А–љ—Г—О —З–∞—Б—В–Њ—В—Г –±—Л–ї–∞ –њ—А–Є–љ—П—В–∞ —З–∞—Б—В–Њ—В–∞ –≤ 440 –У—Ж, —Е–Њ—В—П –≤ —А–∞–Ј–љ–Њ–µ –≤—А–µ–Љ—П –≤ –Ї–∞—З–µ—Б—В–≤–µ –Њ–њ–Њ—А–љ–Њ–є —З–∞—Б—В–Њ—В—Л –њ—А–Є–љ–Є–Љ–∞–ї–Є—Б—М —Е–Њ—В—М –Є –±–ї–Є–Ј–Ї–Є–µ, –љ–Њ –Њ—В–ї–Є—З–∞—О—Й–Є–µ—Б—П —З–∞—Б—В–Њ—В—Л. –Ф–Њ —Б–µ–≥–Њ–і–љ—П—И–љ–µ–≥–Њ –і–љ—П —Б—Г—Й–µ—Б—В–≤—Г—О—В –Є –Њ—В–і–µ–ї—М–љ—Л–µ –Љ—Г–Ј—Л–Ї–∞–љ—В—Л –Є –Њ—А–Ї–µ—Б—В—А—Л, –Ї–Њ—В–Њ—А—Л–µ —Б–≤–Њ–Є –Є–љ—Б—В—А—Г–Љ–µ–љ—В—Л –љ–∞—Б—В—А–∞–Є–≤–∞—О—В –Є—Б–њ–Њ–ї—М–Ј—Г—П –≤ –Ї–∞—З–µ—Б—В–≤–µ –Њ–њ–Њ—А–љ–Њ–є —З–∞—Б—В–Њ—В—Л
–Ґ—Г—В —Б—В–Њ–Є—В –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –≤—Б—П —Б—Г—В—М —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ —Б—В—А–Њ—П –љ–µ –≤ –і–µ–ї–µ–љ–Є–Є –Њ–Ї—В–∞–≤—Л –Є–Љ–µ–љ–љ–Њ –љ–∞ 12 –Є–љ—В–µ—А–≤–∞–ї–Њ–≤, –∞ –≤ –і–µ–ї–µ–љ–Є–Є –µ—С –Є–Љ–µ–љ–љ–Њ –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ—Л–µ (—Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П —З–∞—Б—В–Њ—В –Љ–µ–ґ–і—Г –ї—О–±—Л–Љ–Є –і–≤—Г–Љ—П —Б–Њ—Б–µ–і–љ–Є–Љ–Є –љ–Њ—В–∞–Љ–Є –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ –і–ї—П –ї—О–±–Њ–є –њ–∞—А—Л —Б–Њ—Б–µ–і–љ–Є—Е –љ–Њ—В). 12-—Б—В—Г–њ–µ–љ—З–∞—В–Њ–µ –і–µ–ї–µ–љ–Є–µ вАФ —Н—В–Њ –≤—Б–µ–≥–Њ –ї–Є—И—М —З–∞—Б—В–љ—Л–є —Б–ї—Г—З–∞–є (—Е–Њ—В—М –Є –Є–Љ–µ—О—Й–Є–є –∞–±—Б–Њ–ї—О—В–љ–Њ –њ—А–µ–≤–Њ—Б—Е–Њ–і—П—Й–µ–µ –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –і—А—Г–≥–Є–Љ–Є —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є–µ). –°—Г—Й–µ—Б—В–≤—Г—О—В –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П, –љ–∞–њ–Є—Б–∞–љ–љ—Л–µ –і–ї—П —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–є —В–µ–Љ–њ–µ—А–∞—Ж–Є–Є, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–є –Њ–Ї—В–∞–≤–∞ –і–µ–ї–Є—В—Б—П, –Ї –њ—А–Є–Љ–µ—А—Г, –љ–∞ 24 –Є–љ—В–µ—А–≤–∞–ї–∞, –∞ –љ–µ –љ–∞ 12.
–≠—В–Њ—В –Є–љ—В–µ—А–≤–∞–ї –≤ –Њ–і–љ—Г –і–≤–µ–љ–∞–і—Ж–∞—В—Г—О –Њ–Ї—В–∞–≤—Л –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –њ–Њ–ї—Г—В–Њ–љ–Њ–Љ, –∞ –і–≤–µ —В–∞–Ї–Є—Е –Є–љ—В–µ—А–≤–∞–ї–∞ –Њ–±—А–∞–Ј—Г—О—В —Ж–µ–ї—Л–є —В–Њ–љ. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ–Њ–ї—Г—З–∞–µ—В—Б—П, –Њ–Ї—В–∞–≤–∞ –Ї–∞–Ї –Є–љ—В–µ—А–≤–∞–ї —Б–Њ—Б—В–Њ–Є—В –Є–Ј 12 –њ–Њ–ї—Г—В–Њ–љ–Њ–≤ –Є–ї–Є 6 —В–Њ–љ–Њ–≤.
(–Т–Њ–Њ–±—Й–µ-—В–Њ –њ–Њ–ї—Г—В–Њ–љ–∞ вАФ –њ–Њ–љ—П—В–Є–µ –∞–Ї—В—Г–∞–ї—М–љ–Њ –Є –і–ї—П –і—А—Г–≥–Є—Е —Б—В—А–Њ–µ–≤, –і–ї—П —В–Њ–≥–Њ –ґ–µ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–≥–Њ —Б—В—А–Њ—П, —В–Њ–ї—М–Ї–Њ –≤ –љ—С–Љ –µ—Б—В—М —Ж–µ–ї—Л—Е —В—А–Є —В–Є–њ–∞ –љ–µ–Љ–љ–Њ–≥–Њ –Њ—В–ї–Є—З–∞—О—Й–Є—Е—Б—П –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞ –њ–Њ–ї—Г—В–Њ–љ–Њ–≤).–Ґ.–µ. –Є ¬Ђ–Њ–Ї—В–∞–≤–∞¬ї –Є ¬Ђ–њ–Њ–ї—Г—В–Њ–љ¬ї —П–≤–ї—П—О—В—Б—П –µ–і–Є–љ–Є—Ж–∞–Љ–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П –Є –≤ –њ—А–Є–љ—Ж–Є–њ–µ –Њ–±–ї–∞–і–∞—О—В –Њ–і–љ–Њ–є –Є —В–Њ–є –ґ–µ —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М—О (–±–µ–Ј—А–∞–Ј–Љ–µ—А–љ—Л –Ї–∞–Ї –Є –і–µ—Ж–Є–±–µ–ї).
–Т–Њ–Њ–±—Й–µ, –љ–∞–Ј–≤–∞–љ–Є—П ¬Ђ—В–Њ–љ–Њ–≤¬ї –Є ¬Ђ–њ–Њ–ї—Г—В–Њ–љ–Њ–≤¬ї, –ї–∞—В–Є–љ—Б–Ї–Њ–µ ¬Ђ–≤–Њ—Б–µ–Љ—М¬ї (oct) –≤ –Ї–Њ—А–љ–µ —Б–ї–Њ–≤–∞ ¬Ђ–Њ–Ї—В–∞–≤–∞¬ї –Є —В—А–∞–і–Є—Ж–Є—П –љ–∞–ї–Є—З–Є—П –Є –Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ–≥–Њ —Б–њ–Њ—Б–Њ–±–∞ –Ї–Њ–Љ–±–Є–љ–Є—А–Њ–≤–∞–љ–Є—П –љ–∞ –Ї–ї–∞–≤–Є–∞—В—Г—А–∞—Е –Ї–ї–∞–≤–Є—И–љ—Л—Е –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞—Е —З–µ—А–љ—Л—Е –Є –±–µ–ї—Л—Е –Ї–ї–∞–≤–Є—И –≤–Њ—Б—Е–Њ–і—П—В –Ї –њ–µ—А–Є–Њ–і–∞–Љ, –Ї–Њ–≥–і–∞ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є—Б—М –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ—Л–µ —Б—В—А–Њ–Є, –≤ —Б–≤—П–Ј–Є —Б —З–µ–Љ –Є–љ—В–µ—А–≤–∞–ї –Љ–µ–ґ–і—Г —Б–Њ—Б–µ–і–љ–µ–є –±–µ–ї–Њ–є –Є —Б–Њ—Б–µ–і–љ–µ–є —З—С—А–љ–Њ–є –Ї–ї–∞–≤–Є—И–∞–Љ–Є –±—Л–ї –±—Л–ї –Њ—В–ї–Є—З–µ–љ –Њ—В –њ–Њ–і–µ–ї–µ–љ–љ–Њ–≥–Њ –љ–∞ –і–≤–∞ –Є–љ—В–µ—А–≤–∞–ї–∞ –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –±–µ–ї—Л–Љ–Є –Ї–ї–∞–≤–Є—И–∞–Љ–Є. –° –≤–≤–µ–і–µ–љ–Є–µ–Љ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ —Б–Љ—Л—Б–ї–∞ –њ–Њ –Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ –і–µ–ї–µ–љ–Є–µ –Ї–ї–∞–≤–Є—И –љ–∞ —З—С—А–љ—Л–µ –Є –±–µ–ї—Л–µ –њ–Њ—В–µ—А—П–ї–Њ –≤—Б—П–Ї–Є–є —Б–Љ—Л—Б–ї (–Ї—А–Њ–Љ–µ —Г–і–Њ–±—Б—В–≤–∞ –Є –Є—Б—В–Њ—А–Є—З–µ—Б–Ї–Є —Б–ї–Њ–ґ–Є–≤—И–µ–є—Б—П —В—А–∞–і–Є—Ж–Є–Є), –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤—Б–µ –Ї–ї–∞–≤–Є—И–Є —А–∞–≤–љ–Њ–Ј–љ–∞—З–љ—Л –Є –Є–љ—В–µ—А–≤–∞–ї—Л –Љ–µ–ґ–і—Г —З–∞—Б—В–Њ—В–∞–Љ–Є –ї—О–±—Л—Е –і–≤—Г—Е —Б–Њ—Б–µ–і–љ–Є—Е –Ї–ї–∞–≤–Є—И вАФ –Є–і–µ–љ—В–Є—З–љ—Л.
–Я–Њ—Н—В–Њ–Љ—Г:
- –Ґ–Њ, —З—В–Њ –Њ–Ї—В–∞–≤–∞ —Н—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —З–∞—Б—В–Њ—В 1:2 вАФ —Н—В–Њ –Љ–Є—А–Њ–≤–∞—П –Є—Б—В–Є–љ–∞. –Ш—Б—В–Є–љ–∞ —В–∞–Ї–Њ–≥–Њ –ґ–µ –њ–Њ—А—П–і–Ї–∞, –Ї–∞–Ї —З–Є—Б–ї–Њ –Я–Є.
- –Ф–µ–ї–µ–љ–Є–µ –Њ–Ї—В–∞–≤—Л –Є–Љ–µ–љ–љ–Њ –љ–∞ 12 —Б—В—Г–њ–µ–љ–µ–є, –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ —А–∞–≤–љ—Л—Е —Б—В—Г–њ–µ–љ–µ–є –Є –≤—Л–±–Њ—А —З–∞—Б—В–Њ—В—Л 440 –У—Ж вАФ —Н—В–Њ –њ—А–µ–і–Љ–µ—В —Б–Њ–≥–ї–∞—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –ї—О–і—М–Љ–Є. –Х—Б—В—М –і—А—Г–≥–Є–µ —Б–Њ–≥–ї–∞—И–µ–љ–Є—П. –Ю–љ–Є –≤—А—П–і –ї–Є –Љ–µ–љ–µ–µ –њ—А–∞–≤–Є–ї—М–љ—Л–µ –Є –≤—А—П–і –ї–Є –±–Њ–ї–µ–µ –њ—А–∞–≤–Є–ї—М–љ—Л–µ. –Я—А–Њ—Б—В–Њ –Њ–і–љ–Є —Б–Њ–≥–ї–∞—И–µ–љ–Є—П –±–Њ–ї–µ–µ –њ–Њ–њ—Г–ї—П—А–љ—Л, –∞ –і—А—Г–≥–Є–µ вАФ –Љ–µ–љ–µ–µ –њ–Њ–њ—Г–ї—П—А–љ—Л.
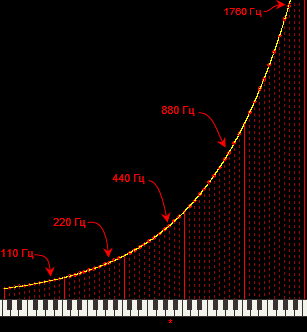
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, –≤ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Љ—Г–Ј—Л–Ї–µ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–µ–µ —Б–Њ–њ–Њ—Б—В–∞–≤–ї–µ–љ–Є–µ –љ–Њ—В –Є —З–∞—Б—В–Њ—В –Є—Е –±–∞–Ј–Њ–≤–Њ–≥–Њ —В–Њ–љ–∞:
–Р –µ—Б–ї–Є –≤–∞–Љ –Є–љ—В–µ—А–µ—Б–љ–Њ, –љ–∞—Б–Ї–Њ–ї—М–Ї–Њ –Њ—В–ї–Є—З–∞—О—В—Б—П —З–∞—Б—В–Њ—В—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –љ–Њ—В –љ–∞—В—Г—А–∞–ї—М–љ–Њ–≥–Њ –Є —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–≥–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ —Б—В—А–Њ–µ–≤:
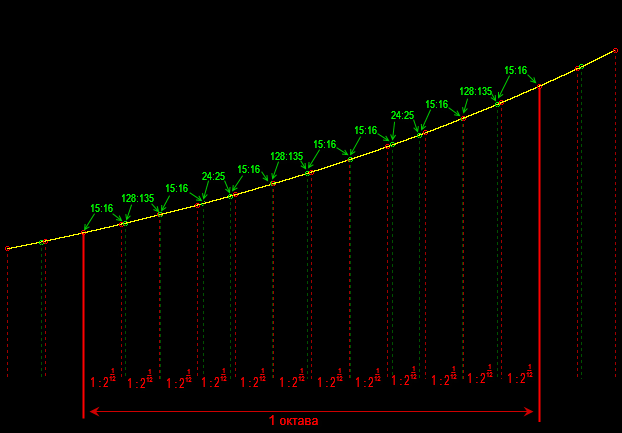
(–Ъ—А–∞—Б–љ—Л–µ –ї–Є–љ–Є–Є –Њ—В–і–µ–ї—П—О—В –Є–љ—В–µ—А–≤–∞–ї—Л —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ —Б—В—А–Њ—П, –∞ –Ї—А–∞—Б–љ—Л–µ –і—А–Њ–±–Є –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—В —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П —З–∞—Б—В–Њ—В —Б–Њ—Б–µ–і–љ–Є—Е –љ–Њ—В. –Ч–µ–ї—С–љ—Л–µ –ї–Є–љ–Є–Є –Є –і—А–Њ–±–Є –≤—Л–њ–Њ–ї–љ—П—О—В –∞–љ–∞–ї–Њ–≥–Є—З–љ—Г—О –Ј–∞–і–∞—З—Г –і–ї—П –љ–∞—В—Г—А–∞–ї—М–љ–Њ–≥–Њ —Б—В—А–Њ—П)
–Э–Њ—В—Л –≤ –њ—А–µ–і–µ–ї–∞—Е –Њ–Ї—В–∞–≤—Л –Є–Љ–µ—О—В —Б–≤–Њ–Є –љ–∞–Ј–≤–∞–љ–Є—П, –Ї–Њ—В–Њ—А—Л–µ –њ—А–Є—Б–≤–∞–Є–≤–∞—О—В—Б—П –љ–Њ—В–∞–Љ –≤ –Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ–є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є, –∞ —Н—В–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М –њ–Њ–≤—В–Њ—А—П–µ—В—Б—П –Ї–∞–ґ–і—Г—О –Њ–Ї—В–∞–≤—Г. –Ю–і–љ–Њ–Є–Љ—С–љ–љ—Л–µ –љ–Њ—В—Л –≤—Б–µ–≥–і–∞ –Є–Љ–µ—О—В –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є –Є–љ—В–µ—А–≤–∞–ї, —А–∞–≤–љ—Л–є —Ж–µ–ї–Њ–Љ—Г —З–Є—Б–ї—Г –Њ–Ї—В–∞–≤, –Є –≤ —Ж–µ–ї–Њ–Љ —В–∞–Ї–Є–µ –љ–Њ—В—Л —Б—З–Є—В–∞—О—В—Б—П –Њ–і–Є–љ–∞–Ї–Њ–≤—Л–Љ–Є —Б —В–Њ—З–љ–Њ—Б—В—М –і–Њ –њ—А–Є–љ–∞–і–ї–µ–ґ–љ–Њ—Б—В–Є –Ї –Њ–Ї—В–∞–≤–∞–Љ. –Т—Л—А–∞–ґ–∞—П—Б—М –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ —П–Ј—Л–Ї–Њ–Љ, —Б—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—В вАФ —Н—В–Њ
—Б—А–∞–≤–љ–µ–љ–Є–µ –њ–Њ –Љ–Њ–і—Г–ї—О 12.
_________________________
–Ф—А—Г–≥–Њ–є –≤–∞–ґ–љ—Л–є —Д–∞–Ї—В –Њ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Є –љ–µ –Њ—З–µ–љ—М –Љ—Г–Ј—Л–Ї–µ: —Б –љ–µ–Ї–Њ—В–Њ—А—Л–Љ —Г–њ—А–Њ—Й–µ–љ–Є–µ–Љ –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М: –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л–µ —Б–Њ—З–µ—В–∞–љ–Є—П –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –Ј–≤—Г—З–∞—Й–Є—Е –љ–Њ—В –Њ–Ї–∞–Ј—Л–≤–∞—О—В –љ–∞ —З–µ–ї–Њ–≤–µ–Ї–∞ —В–Њ—В –Є–ї–Є –Є–љ–Њ–є –њ—Б–Є—Е–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є–є —Н—Д—Д–µ–Ї—В. –Я—А–Њ–Є–Ј–≤–Њ–і–Є–Љ—Л–є —Н—Д—Д–µ–Ї—В –Ј–∞–≤–Є—Б–Є—В –Њ—В –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ –Љ–µ–ґ–і—Г –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –Ј–≤—Г—З–∞—Й–Є–Љ–Є –љ–Њ—В–∞–Љ–Є.
–Ю–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–µ –Ј–≤—Г—З–∞–љ–Є–µ –Ї–∞–Ї –Љ–Є–љ–Є–Љ—Г–Љ —В—А—С—Е –љ–µ–Њ–і–Є–љ–∞–Ї–Њ–≤—Л—Е (!) –љ–Њ—В –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –∞–Ї–Ї–Њ—А–і–Њ–Љ.
–Х—Б—В—М –≤ –Љ—Г–Ј—Л–Ї–µ —В–∞–Ї–Њ–µ –њ–Њ–љ—П—В–Є–µ, –Ї–∞–Ї ¬Ђ–≥–∞—А–Љ–Њ–љ–Є—П¬ї, –Ї–Њ—В–Њ—А–Њ–µ –Є–Љ–µ–µ—В —В—Л—Б—П—З—Г –Ј–љ–∞—З–µ–љ–Є–є, –Њ–і–љ–Њ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е вАФ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —Б–Њ–Ј–≤—Г—З–Є–є. –Ш —Б–∞–Љ–Є —Б–Њ–Ј–≤—Г—З–Є—П, –Є –Є—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М –њ—А–Є —Н—В–Њ–Љ –њ–Њ–і—З–Є–љ–µ–љ—Л –љ–µ–Ї–Њ—В–Њ—А—Л–Љ –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В—П–Љ. –Х—Б–ї–Є —Г–њ—А–Њ—Б—В–Є—В—М –Є –≤—Л–Ї–Є–љ—Г—В—М –Є–Ј —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—П –љ–µ–Ї–Њ—В–Њ—А—Л–µ –љ–µ—Б—В–∞–љ–і–∞—А—В–љ—Л–µ –Є —Н–Ї–Ј–Њ—В–Є—З–µ—Б–Ї–Є–µ –≤–µ—Й–Є, –Љ–Њ–ґ–љ–Њ –≥—А—Г–±–Њ —Б–Ї–∞–Ј–∞—В—М, —З—В–Њ –µ—Б–ї–Є —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М –Ї–∞–Ї–Њ–µ-—В–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ, —В–Њ –њ–Њ–Љ–Є–Љ–Њ –Љ–µ–ї–Њ–і–Є—З–µ—Б–Ї–Њ–є –ї–Є–љ–Є–Є –≤ –љ—С–Љ —П–≤–љ–Њ –Є–ї–Є –љ–µ—П–≤–љ–Њ –њ—А–Є—Б—Г—В—Б—В–≤—Г–µ—В –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М –∞–Ї–Ї–Њ—А–і–Њ–≤, –≤ –њ–Њ–і—З–Є–љ–µ–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–є –љ–∞—Е–Њ–і—П—В—Б—П —В–∞–Ї –Є–ї–Є –Є–љ–∞—З–µ –≤—Б–µ –њ–∞—А—В–Є–Є –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П. –Э–µ—А–µ–і–Ї–Њ —Н—В–Є –∞–Ї–Ї–Њ—А–і—Л —Б–∞–Љ–Є —П–≤–ї—П—О—В—Б—П —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ–є –њ–∞—А—В–Є–µ–є –≤ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–Є.
__________________________
–Ъ —Б–Њ–ґ–∞–ї–µ–љ–Є—О, –њ—А–Є—И–ї–Њ—Б—М —А–∞—Б—Б–Ї–∞–Ј–∞—В—М –Ї—Г—З—Г –≤–µ—Й–µ–є, —Е–Њ—В—П –Є –Є—Е –њ—А–Є—И–ї–Њ—Б—М —Г–њ—А–Њ—Б—В–Є—В—М, –Є–љ–∞—З–µ –і–∞–ї—М–љ–µ–є—И–Є–є —А–∞—Б—Б–Ї–∞–Ј –Є–Љ–µ–ї –±—Л —Б–Љ—Л—Б–ї —В–Њ–ї—М–Ї–Њ –і–ї—П, –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ, –њ–∞—А—Л —З–µ–ї–Њ–≤–µ–Ї, –Ї–Њ—В–Њ—А—Л–µ –Є —В–∞–Ї –≤—Б—С —Н—В–Њ –Ј–љ–∞–ї–Є.
_________________________
–Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–є –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А —Б–њ–µ–Ї—В—А–∞ –і–µ–ї–∞–µ—В FFT (–Є–ї–Є –љ–µ FFT, –љ–Њ —Н—В–Њ –љ–µ —В–∞–Ї —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ —Б–µ–є—З–∞—Б) –Є –Њ—В–Њ–±—А–∞–ґ–∞–µ—В –њ–Њ–ї—Г—З–µ–љ–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В –≤ –≤–Є–і–µ –≥—А–∞—Д–Є–Ї–∞ –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В:
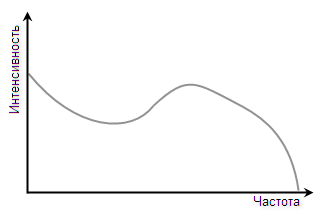
X-–Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ –Њ–Ј–љ–∞—З–∞–µ—В —З–∞—Б—В–Њ—В—Г, Y-–Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ вАФ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М. –ѓ —Б–њ–µ—Ж–Є–∞–ї—М–љ–Њ –љ–∞–њ–Є—Б–∞–ї —Б–ї–Њ–≤–Њ ¬Ђ–Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М¬ї, –∞ –љ–µ, –Ї –њ—А–Є–Љ–µ—А—Г, ¬Ђ–∞–Љ–њ–ї–Є—В—Г–і–∞¬ї, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –≤ –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ —Н—В–Њ –Є–Љ–µ–љ–љ–Њ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М, –Ї–Њ—В–Њ—А–∞—П –Љ–Њ–ґ–µ—В –Њ–Ј–љ–∞—З–∞—В—М –Є –∞–Љ–њ–ї–Є—В—Г–і—Г, –Є —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї—Г—О –Љ–Њ—Й–љ–Њ—Б—В—М —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–є —Б–Њ—Б—В–∞–≤–ї—П—О—Й–µ–є, –Є —Г—А–Њ–≤–µ–љ—М –≤ –і–µ—Ж–Є–±–µ–ї–∞—Е –Є —З—В–Њ-–љ–Є–±—Г–і—М –µ—Й—С.
–І—В–Њ –Ї–∞—Б–∞–µ—В—Б—П –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Њ–є –Њ—Б–Є, –Њ–Ј–љ–∞—З–∞—О—Й–µ–є —З–∞—Б—В–Њ—В–љ—Г—О –Њ–±–ї–∞—Б—В—М, –Љ–Њ–ґ–µ—В –њ—А–Є–Љ–µ–љ—П—В—М—Б—П –ї–Є–±–Њ –ї–Є–љ–µ–є–љ—Л–є –Љ–∞—Б—И—В–∞–±:
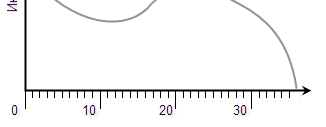
–Ы–Є–±–Њ –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Є–є:
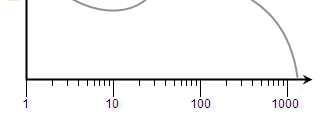
–Э–∞—Б, –њ–Њ–љ—П—В–љ–Њ–µ –і–µ–ї–Њ, –Є–љ—В–µ—А–µ—Б—Г–µ—В –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Є–є –Љ–∞—Б—И—В–∞–±, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –њ—А–Є –љ—С–Љ –ї—О–±–∞—П –Њ–Ї—В–∞–≤–∞, —В–Њ–љ –Є–ї–Є –њ–Њ–ї—Г—В–Њ–љ –Є–ї–Є —Ж–µ–љ—В—А (—Ж–µ–љ—В вАФ –Њ–і–љ–∞ —Б–Њ—В–∞—П –њ–Њ–ї—Г—В–Њ–љ–∞ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ —Б—В—А–Њ—П) –Є–Љ–µ—О—В –Њ–і–Є–љ–∞–Ї–Њ–≤—Г—О —И–Є—А–Є–љ—Г –љ–∞ –≥—А–∞—Д–Є–Ї–µ.
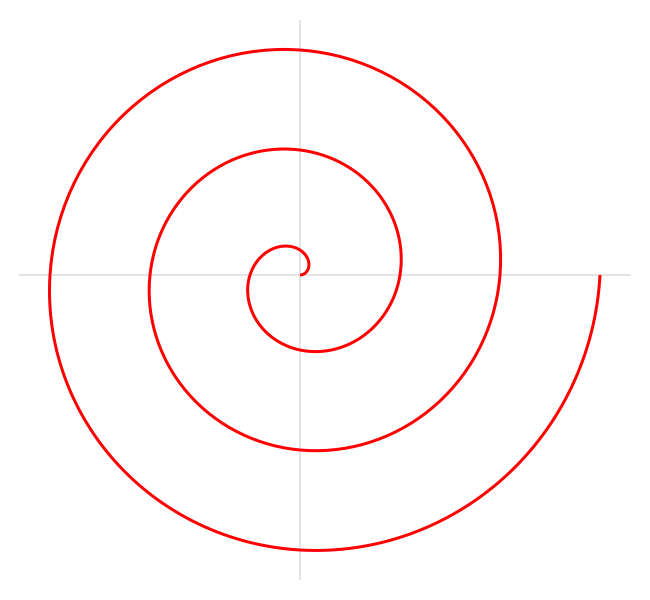
–Ш—В–∞–Ї, –Љ–Њ—П –Є–Ј–љ–∞—З–∞–ї—М–љ–∞—П –Є–і–µ—П –њ—А–µ–і–µ–ї—М–љ–Њ –њ—А–Њ—Б—В–∞:
–Ш—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Є–є –Љ–∞—Б—И—В–∞–±, –љ–Њ –≤–Љ–µ—Б—В–Њ –і–µ–Ї–∞—А—В–Њ–≤—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –њ–Њ–ї—П—А–љ—Л–µ.–Ґ–Њ, —З—В–Њ –≤ –і–µ–Ї–∞—А—В–Њ–≤—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –±—Л–ї–Њ
x-–Ї–Њ–Њ—А–і–Є–љ–∞—В–Њ–є, вАФ —Б—В–∞–љ–µ—В —Г–≥–ї–Њ–≤–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В–Њ–є.
–Ґ–Њ, —З—В–Њ –≤ –і–µ–Ї–∞—А—В–Њ–≤—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –±—Л–ї–Њ
y-–Ї–Њ–Њ—А–і–Є–љ–∞—В–Њ–є, вАФ —Б—В–∞–љ–µ—В —А–∞–і–Є–∞–ї—М–љ–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В–Њ–є.
–Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, —А–∞–і–Є–∞–ї—М–љ–∞—П –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ –±—Г–і–µ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є, –∞ —Г–≥–ї–∞–≤–∞—П –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ вАФ –ї–Њ–≥–∞—А–Є—Д–Љ—Г —З–∞—Б—В–Њ—В—Л —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–є —Б–Њ—Б—В–∞–≤–ї—П—О—Й–µ–є –њ–Њ –Њ—Б–љ–Њ–≤–∞–љ–Є—О 2. –Я—А–Є—З—С–Љ –і–ї—П —Г–≥–ї–Њ–≤–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є
–і–Њ–ї–ґ–µ–љ –±—Л—В—М –≤—Л–±—А–∞–љ —В–∞–Ї–Є–Љ, —З—В–Њ–±—Л –љ–∞ –Њ–і–Є–љ –Њ–±–Њ—А–Њ—В –њ—А–Є—Е–Њ–і–Є–ї–∞—Б—М –Њ–і–љ–∞ –Њ–Ї—В–∞–≤–∞.
–≠—В–Њ –∞–±—Б–Њ–ї—О—В–љ—Л–є –Љ–Є–љ–Є–Љ—Г–Љ –Є–Ј–ї–Њ–ґ–µ–љ–Є—П –Љ–Њ–µ–є –Є–і–µ–Є, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –і–∞–ї—М—И–µ —Г –љ–µ—С –µ—Б—В—М —А–∞–Ј–≤–Є—В–Є–µ –Є —Б–Њ–њ—Г—В—Б—В–≤—Г—О—Й–Є–µ –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П –Є —В—А–µ–±–Њ–≤–∞–љ–Є—П, –љ–Њ –њ–Њ–Ї–∞ –Њ–≥—А–∞–љ–Є—З–Є–Љ—Б—П —Н—В–Є–Љ.
–І—В–Њ —Н—В–Њ –і–∞—С—В?
–Ь—Г–Ј—Л–Ї–∞–ї—М–љ—Л–µ –Є–љ—В–µ—А–≤–∞–ї—Л –њ—А–µ–≤—А–∞—Й–∞—О—В—Б—П –≤ —Г–≥–ї—Л!
–Я–Њ–ї—Г—В–Њ–љ –њ—А–µ–≤—А–∞—Й–∞–µ—В—Б—П –≤ 30¬∞, —В–Њ–љ вАФ –≤ 60¬∞. –¶–µ–љ—В вАФ –≤ 0.3¬∞.
–Ю–Ї—В–∞–≤–∞ –њ—А–µ–≤—А–∞—Й–∞–µ—В—Б—П –≤ –њ–Њ–ї–љ—Л–є –Њ–±–Њ—А–Њ—В вАФ 360¬∞.
–Э–Њ—В–∞ ¬Ђ–Ф–Њ¬ї¬†—Б–∞–Љ–Њ–є –љ–Є–Ј–Ї–Њ–є –Њ–Ї—В–∞–≤—Л –Є –љ–Њ—В–∞ ¬Ђ–Ф–Њ¬ї —Б–∞–Љ–Њ–є –≤—Л—Б–Њ–Ї–Њ–є –Њ–Ї—В–∞–≤—Л (—А–∞–≤–љ–Њ –Ї–∞–Ї –Є –љ–Њ—В–∞ ¬Ђ–Ф–Њ¬ї –≤–Њ–Њ–±—Й–µ –ї—О–±–Њ–є –Њ–Ї—В–∞–≤—Л) –≤ –њ–Њ–ї—П—А–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –ї—Г—З—Г –Є–Љ–µ—О—Й–Є–Љ—Г –Њ–і–Є–љ –Є —В–Њ—В –ґ–µ —Г–≥–Њ–ї –љ–∞–Ї–ї–Њ–љ–∞, –Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –≤—Б–µ —Н—В–Є –љ–Њ—В—Л –Њ—В–Њ–±—А–∞–ґ–∞—О—В—Б—П –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ.
–Э–∞ –і–∞–љ–љ–Њ–Љ —Н—В–∞–њ–µ —Н—В–Њ—В —Д–∞–Ї—В–Њ—А (–Њ–і–Є–љ–∞–Ї–Њ–≤—Л–µ –љ–Њ—В—Л —А–∞–Ј–љ—Л—Е –Њ–Ї—В–∞–≤ –љ–∞–Ї–ї–∞–і—Л–≤–∞—О—В—Б—П –Є —Б–ї–Є–≤–∞—О—В—Б—П –≤ –Њ–і–љ—Г –њ—А–Є –њ–Њ–ї—П—А–љ–Њ–Љ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–Є) –Љ–Њ–ґ–µ—В —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М –Ї–∞–Ї –љ–µ–і–Њ—Б—В–∞—В–Њ–Ї —В–∞–Ї–Њ–≥–Њ —Б–њ–Њ—Б–Њ–±–∞ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є—П, –љ–Њ –њ–Њ–і–Њ–ґ–і–Є—В–µ, –Њ–± —Н—В–Њ–Љ –±—Г–і–µ—В —Б–Ї–∞–Ј–∞–љ–Њ –і–∞–ї—М—И–µ.
–Я–Њ–Ї–∞ –ґ–µ вАФ –Љ–∞–ї–µ–љ—М–Ї–Є–є –њ—А–Є–Љ–µ—А.
–°–њ–µ–Ї—В—А –Њ—А–≥–∞–љ–∞ (–Ј–≤—Г—З–Є—В –љ–Њ—В–∞ ¬Ђ–Ф–Њ¬ї):
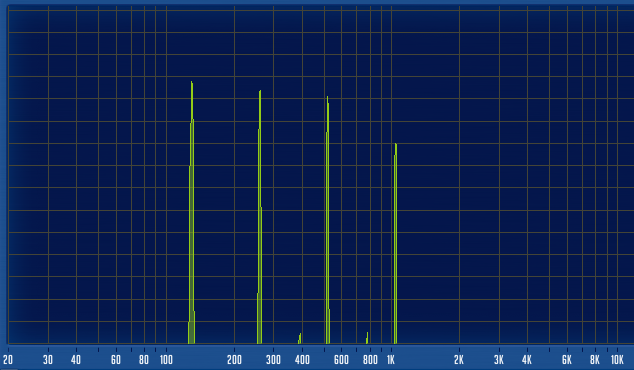
–Э–∞ —Н—В–Њ–є —Б–њ–µ–Ї—В—А–Њ–≥—А–∞–Љ–Љ–µ —Е–Њ—А–Њ—И–Њ –≤–Є–і–љ–Њ –±–∞–Ј–Њ–≤—Л–є —В–Њ–љ –Є –Њ–±–µ—А—В–Њ–љ—Л. –Я—А–Є—З—С–Љ –≤–Є–і–љ–Њ, —З—В–Њ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М 1-–≥–Њ,3-–≥–Њ –Є 7-–≥–Њ –Њ–±–µ—А—В–Њ–љ–Њ–≤ вАФ –≤—Л—Б–Њ–Ї–∞—П, –∞ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М 2-–≥–Њ, 4-–≥–Њ, 5-–≥–Њ, 6-–≥–Њ, 8-–≥–Њ –Є –њ–Њ—Б–ї–µ–і—Г—О—Й–Є—Е –Њ–±–µ—А—В–Њ–љ–Њ–≤ вАФ –Є–ї–Є –љ–µ–Ј–љ–∞—З–Є—В–µ–ї—М–љ–∞—П, –Є–ї–Є –љ–µ—А–∞–Ј–ї–Є—З–Є–Љ–Њ –Љ–∞–ї–∞—П.
–§–∞–Ї—В–Є—З–µ—Б–Ї–Є, –Љ—Л –≤—Л –≤–Є–і–Є–Љ —З–µ—В—Л—А–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є (–≥–∞—А–Љ–Њ–љ–Є–Ї–∞ вАФ —Б–њ–µ–Ї—В—А–∞–ї—М–љ–∞—П —Б–Њ—Б—В–∞–≤–ї—П—О—Й–∞—П), –Њ—В—Б—В–∞—О—Й–Є–µ –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞ –љ–∞ –Њ–і–љ—Г –Њ–Ї—В–∞–≤—Г.
–Х—Б–ї–Є –±—Л –Љ—Л —Б–Љ–Њ—В—А–µ–ї–Є –љ–∞ —Б–њ–µ–Ї—В—А –Њ–≥—А–∞–љ–љ–Њ–≥–Њ –Ј–≤—Г–Ї–∞ –≤ —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–Љ –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–µ, –Є—Б–њ–Њ–ї—М–Ј—Г—О—Й–Є–Љ –њ–Њ–ї—П—А–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –і–ї—П —З–∞—Б—В–Њ—В—Л, –Љ—Л –±—Л —Г–≤–Є–і–µ–ї–Є 4 –љ–∞–ї–Њ–ґ–Є–≤—И–Є—Е—Б—П –і—А—Г–≥ –љ–∞ –і—А—Г–≥–∞ –ї–µ–њ–µ—Б—В–Ї–∞.
–І—В–Њ –Ї–∞—Б–∞–µ—В—Б—П —В–µ—А–Љ–Є–љ–∞ ¬Ђ–ї–µ–њ–µ—Б—В–Њ–Ї¬ї. –Т –љ–µ–Ї–Њ—В–Њ—А—Л—Е –Ї—А—Г–≥–∞—Е —Н—В–Њ –≤–µ—Б—М–Љ–∞ –Ј–љ–∞–Ї–Њ–Љ—Л–є –Є —З–∞—Б—В–Њ-–Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Л–є —В–µ—А–Љ–Є–љ, –њ—А–Є—З—С–Љ –Ї–∞–Ї –≤ –Њ—В–љ–Њ—И–µ–љ–Є–Є –њ–Њ–ї—П—А–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В–∞–Ї –Є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е.
–Т–Њ–Њ–±—Й–µ –ґ–µ –љ–∞ –Є–і–µ—О –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П –њ–Њ–ї—П—А–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В –Љ–µ–љ—П –њ–Њ–і—В–Њ–ї–Ї–љ—Г–ї–∞ —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В—М –і–≤—Г—Е –≤–µ—Й–µ–є:
- –Ю—Б–Њ–Ј–љ–∞–љ–Є–µ –Њ—Б–Њ–±–Њ–є —А–Њ–ї–Є —В–∞–Ї–Њ–≥–Њ –Є–љ—В–µ—А–≤–∞–ї–∞, –Ї–∞–Ї ¬Ђ–Њ–Ї—В–∞–≤–∞¬ї, –Њ—Б–Њ–Ј–љ–∞–љ–Є–µ —В–Њ–≥–Њ —Д–∞–Ї—В–∞, —З—В–Њ —Б—А–µ–і–Є —А—П–і–∞ –Њ–±–µ—А—В–Њ–љ–љ—Л—Е –≥–∞—А–Љ–Њ–љ–Є–Ї –Љ–љ–Њ–≥–Є–µ —З–∞—Б—В–Њ—В—Л –Њ—В—Б—В–∞—О—В –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞ —А–Њ–≤–љ–Њ –љ–∞ –Њ–Ї—В–∞–≤—Г, –∞ —Г —В–µ–Љ–±—А–Њ–≤ –љ–µ–Ї–Њ—В–Њ—А—Л—Е –Є–љ—Б—В—А—Г–Љ–µ–љ—В–Њ–≤ (–љ–∞–њ—А–Є–Љ–µ—А –Њ—А–≥–∞–љ–∞) –≤—Б–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є —В–Њ–ї—М–Ї–Њ –Є —Б–Є–і—П—В –љ–∞ –Њ–Ї—В–∞–≤–љ–Њ–є —Б–µ—В–Ї–µ.
- –Я–ї–Њ—В–љ–Њ–µ –Ј–љ–∞–Ї–Њ–Љ—Б—В–≤–Њ –Є —З–∞—Б—В–Њ–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–љ–Є–µ –і–Є–∞–≥—А–∞–Љ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–љ–Њ—Б—В–Є/–≤–Њ—Б–њ—А–Є–Є–Љ—З–Є–≤–Њ—Б—В–Є (–∞–љ—В–µ–љ–љ, –Є–Ј–ї—Г—З–∞—В–µ–ї–µ–є, –њ—А–Є—С–Љ–љ–Є–Ї–Њ–≤).
–Т–Њ—В –љ–∞–њ—А–Є–Љ–µ—А, –і–Є–∞–≥—А–∞–Љ–Љ–∞ –љ–∞–њ—А–∞–≤–ї–µ–љ–љ–Њ—Б—В–Є –∞–љ—В–µ–љ–љ—Л:
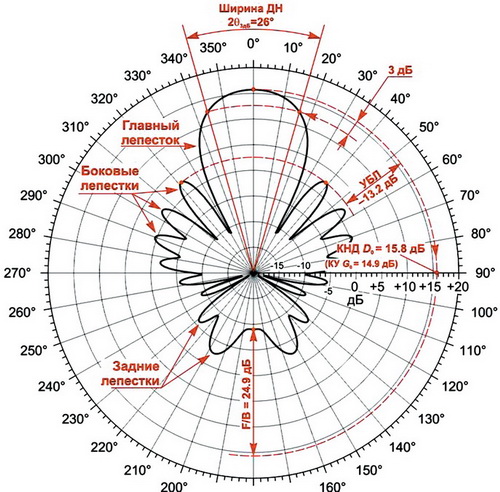
–Э–∞–і–µ—О—Б—М, –њ–Њ—Б–ї–µ —Н—В–Њ–є –Ї–∞—А—В–Є–љ–Ї–Є –Ї–∞–Ї –Љ–Є–љ–Є–Љ—Г–Љ –њ–Њ–љ—П—В–љ–Њ, —З—В–Њ –њ–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–µ—В—Б—П –њ–Њ–і —В–µ—А–Љ–Є–љ–Њ–Љ ¬Ђ–ї–µ–њ–µ—Б—В–Њ–Ї¬ї.
–Ґ–µ–њ–µ—А—М –≤–µ—А–љ—С–Љ—Б—П –Ї —Б–њ–µ–Ї—В—А—Г –Њ—А–≥–∞–љ–∞. –Ґ–µ —З–µ—В—Л—А–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є, –Ї–Њ—В–Њ—А—Л–µ –≤ –љ—С–Љ –њ—А–Є—Б—Г—В—Б—В–≤—Г—О—В (—Б–ї–∞–±–Њ –њ—А–Њ—П–≤–ї—П—О—Й–Є–µ—Б—П вАФ –љ–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ), –љ–∞ –њ–Њ–ї—П—А–љ–Њ–Љ –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–µ –±—Г–і—Г—В –≤—Л–≥–ї—П–і–µ—В—М –≤–Њ—В —В–∞–Ї:
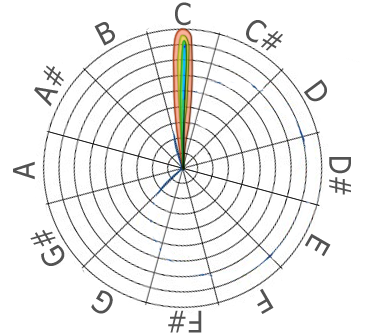 (–Ы–∞—В–Є–љ—Б–Ї–Є–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П: —Б—В–∞–љ–і–∞—А—В–љ—Л–µ –ї–∞—В–Є–љ—Б–Ї–Є–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –љ–Њ—В вАФ –±—Г–Ї–≤–∞ ¬ЂA¬ї
(–Ы–∞—В–Є–љ—Б–Ї–Є–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П: —Б—В–∞–љ–і–∞—А—В–љ—Л–µ –ї–∞—В–Є–љ—Б–Ї–Є–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –љ–Њ—В вАФ –±—Г–Ї–≤–∞ ¬ЂA¬ї
–і–ї—П ¬Ђ–Ы—П¬ї –Є –і–∞–ї–µ–µ –њ–Њ –∞–ї—Д–∞–≤–Є—В—Г –і–Њ —Б–ї–µ–і—Г—О—Й–µ–є –љ–Њ—В—Л ¬Ђ–Ы—П¬ї.
–Ю–і–Є–љ —Б–µ–Ї—В–Њ—А —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Њ–і–љ–Њ–Љ—Г –њ–Њ–ї—Г—В–Њ–љ—Г).
–Ъ—А–∞—Б–Є–≤–Њ, –њ—А–∞–≤–і–∞?
–Ґ–µ–њ–µ—А—М –Њ—З–µ–љ—М –≤–∞–ґ–љ—Л–є –Љ–Њ–Љ–µ–љ—В.–Т—Л—И–µ —П –Њ—В–Љ–µ—В–Є–ї, —З—В–Њ –µ—Б–ї–Є –±—Л –ї–µ–њ–µ—Б—В–Ї–Є –њ—А–Њ—Б—В–Њ –љ–∞–Ї–ї–∞–і—Л–≤–∞–ї–Є—Б—М –і—А—Г–≥ –љ–∞ –і—А—Г–≥–∞, —Н—В–Њ –±—Л–ї–Њ –±—Л –љ–µ –Њ—З–µ–љ—М —Е–Њ—А–Њ—И–Њ: –Љ—Л –±—Л –њ–Њ—В–µ—А—П–ї–Є –Љ–љ–Њ–≥–Њ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –љ–µ —Б–Љ–Њ–≥–ї–Є –±—Л –Њ—В–ї–Є—З–Є—В—М –љ–Њ—В—Г, –Є–≥—А–∞–µ–Љ—Г—О –±–µ–і–љ—Л–Љ —Б–Є–љ—Г—Б–љ—Л–Љ —В–µ–Љ–±—А–Њ–Љ –Њ—В —В–Њ–є –ґ–µ –љ–Њ—В—Л, –Є–≥—А–∞–µ–Љ–Њ–є –Њ—А–≥–∞–љ–љ—Л–Љ —В–µ–Љ–±—А–Њ–Љ.
–Я–Њ—Н—В–Њ–Љ—Г –≤–∞–ґ–љ–∞—П –≤–µ—Й—М, –Ї–Њ—В–Њ—А—Г—О —П —Е–Њ—З—Г –њ–Њ—Б—В—Г–ї–Є—А–Њ–≤–∞—В—М: –Њ—Б–Њ–±—Л–µ –њ—А–∞–≤–Є–ї–∞ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є—П –љ–∞–ї–Њ–ґ–µ–љ–Є—П –ї–µ–њ–µ—Б—В–Ї–Њ–≤.
–Ю–љ–Є —Б–Њ—Б—В–Њ—П—В –Є–Ј –і–≤—Г—Е –њ—Г–љ–Ї—В–Њ–≤:
- –Ы–µ–њ–µ—Б—В–Ї–Є –љ–µ –Є–Љ–µ—О—В –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ–≥–Њ —Ж–≤–µ—В–∞. –¶–≤–µ—В –ї–µ–њ–µ—Б—В–Ї–∞ –Ј–∞–≤–Є—Б–Є—В –Њ—В —З–∞—Б—В–Њ—В—Л (—В.–µ. –≤—Л—Б–Њ—В—Л —В–Њ–љ–∞). –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ —З–∞—Б—В–Њ—В–∞ –≤–ї–Є—П–µ—В –љ–µ —В–Њ–ї—М–Ї–Њ –љ–∞ —Г–≥–ї–Њ–≤—Г—О –Ї–Њ–Њ—А–і–Є–љ–∞—В—Г, –љ–Њ –Є –љ–∞ —Ж–≤–µ—В –ї–µ–њ–µ—Б—В–Ї–∞.
- –Ы–µ–њ–µ—Б—В–Ї–Є –љ–µ —П–≤–ї—П—О—В—Б—П –љ–µ–њ—А–Њ–Ј—А–∞—З–љ—Л–Љ–Є. –Я—А–Њ–Ј—А–∞—З–љ–Њ—Б—В—М –ї–µ–њ–µ—Б—В–Ї–∞ –і–Њ–ї–ґ–љ–∞ –Є–Љ–µ—В—М –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –Њ—В –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–є —Б–Њ—Б—В–∞–≤–ї—П—О—Й–µ–є. –ѓ –љ–µ –≥–Њ–≤–Њ—А—О –Њ —В–Њ–Љ, —З—В–Њ —Н—В–Њ –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –њ–Њ–ї–љ–∞—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М, –љ–Њ –і–Њ–ї–ґ–µ–љ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞—В—М –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л–є –≤–µ—Б–Њ–≤–Њ–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞—О—Й–Є–є —В–∞–Ї—Г—О –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М. –Я—А–Є–≤–µ—В—Б—В–≤—Г–µ—В—Б—П –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –Є–Ј–Љ–µ–љ—П—В—М —Н—В–Њ—В –≤–µ—Б–Њ–≤–Њ–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В.
- –Ю—Б–Њ–±–Њ–µ –њ—А–∞–≤–Є–ї–Њ —Ж–≤–µ—В–Њ–≤–Њ–≥–Њ –љ–∞–ї–Њ–ґ–µ–љ–Є—П: –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –ї–µ–њ–µ—Б—В–Ї–Є –њ–Њ–ї—Г–њ—А–Њ–Ј—А–∞—З–љ—Л, –≤ –Љ–µ—Б—В–∞—Е –љ–∞–ї–Њ–ґ–µ–љ–Є—П –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –Ї–Њ–љ–µ—З–љ—Л–є —Ж–≤–µ—В —В–Њ—З–Ї–Є –і–Њ–ї–ґ–µ–љ –Њ–њ—А–µ–і–µ–ї—П—В—М—Б—П –њ–Њ –∞–і–і–Є—В–Є–≤–љ—Л–Љ –њ—А–∞–≤–Є–ї–∞–Љ —Б–Є–љ—В–µ–Ј–∞ —Ж–≤–µ—В–∞. –Э–µ —Б—В–Њ–Є—В –њ—Г—В–∞—В—М —Н—В–Њ –Њ–±—Л—З–љ—Л–Љ –љ–∞–ї–Њ–ґ–µ–љ–Є–µ–Љ –њ–Њ–ї—Г–њ—А–Њ–Ј—А–∞—З–љ—Л—Е —Ж–≤–µ—В–Њ–≤—Л—Е —Б–ї–Њ—С–≤: –њ—А–Є –њ—А–Њ—Б—В–Њ–Љ –љ–∞–ї–Њ–ґ–µ–љ–Є–Є –њ–Њ—А—П–і–Њ–Ї —Б–ї–µ–і–Њ–≤–∞–љ–Є—П —Б–ї–Њ—С–≤ –Є–≥—А–∞–µ—В —А–Њ–ї—М, –≤ —В–Њ –≤—А–µ–Љ—П –Ї–∞–Ї –њ—А–Є –∞–і–і–Є—В–Є–≤–љ–Њ–Љ —Б–ї–Њ–ґ–µ–љ–Є–Є (–њ—А–Њ—Б—В–Є—В–µ –Ј–∞ —В–∞–Ї—Г—О —В–∞–≤—В–Њ–ї–Њ–≥–Є—О) —Ж–≤–µ—В–Њ–≤—Л–µ –Њ–њ–µ—А–∞–љ–і—Л, —В–∞–Ї —Б–Ї–∞–Ј–∞—В—М, –Ї–Њ–Љ–Љ—Г—В–∞—В–Є–≤–љ—Л, —В.–µ. –њ–Њ—А—П–і–Њ–Ї —Б–ї–∞–≥–∞–µ–Љ—Л—Е –љ–µ –Є–≥—А–∞–µ—В –љ–Є–Ї–∞–Ї–Њ–є —А–Њ–ї–Є. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –±–∞–Ј–Њ–≤—Л–є —В–Њ–љ –Њ–і–љ–Њ–є –Є —В–Њ–є –ґ–µ –љ–Њ—В—Л, –љ–Њ —Б—Л–≥—А–∞–љ–љ–Њ–є –≤ —А–∞–Ј–љ—Л—Е –Њ–Ї—В–∞–≤–∞—Е, –±—Г–і–µ—В –Є–Љ–µ—В—М –ї–µ–њ–µ—Б—В–Њ–Ї —А–∞–Ј–љ—Л—Е —Ж–≤–µ—В–Њ–≤. –Т–∞–ґ–љ–Њ–µ –њ—А–∞–≤–Є–ї–Њ: –µ—Б–ї–Є —Б—Л–≥—А–∞—В—М –Њ–і–љ—Г –Є —В—Г –ґ–µ –љ–Њ—В—Г –≤–Њ –≤—Б–µ—Е –Њ–Ї—В–∞–≤–∞—Е –Є–Ј —Б–ї—Л—И–Є–Љ–Њ–≥–Њ –і–ї—П —З–µ–ї–Њ–≤–µ–Ї–∞ –і–Є–∞–њ–∞–Ј–Њ–љ–∞ вАФ –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —Б–ї–Њ–ґ–µ–љ–Є—П –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –і–Њ–ї–ґ–µ–љ –њ–Њ–ї—Г—З–Є—В—М—Б—П –±–µ–ї—Л–є –ї–µ–њ–µ—Б—В–Њ–Ї.
- –°–Є–љ–µ—А–≥–Є—З–µ—Б–Ї–Є–є —Н—Д—Д–µ–Ї—В –ї–µ–њ–µ—Б—В–Ї–Њ–≤: –і–ї—П –≤—Б–µ–≥–Њ –≤—Б–µ–≥–Њ –Ї—А—Г–≥–Њ–≤–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ –і–Њ–ї–ґ–µ–љ –±—Л—В—М –њ–Њ–і—Б—З–Є—В–∞–љ –Ї–∞–Ї —П –µ–≥–Њ –љ–∞–Ј—Л–≤–∞—О ¬Ђ—Б–Є–љ–µ—А–≥–Є—З–µ—Б–Ї–Є–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В¬ї. –І–µ–Љ –±–Њ–ї—М—И–µ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≥–∞—А–Љ–Њ–љ–Є–Ї –њ—А–Є—Е–Њ–і–Є—В—Б—П –љ–∞ –і–∞–љ–љ—Г—О —Г–≥–ї–Њ–≤—Г—О –Ї–Њ–Њ—А–і–Є–љ–∞—В—Г –Є —З–µ–Љ –Є–љ—В–µ–љ—Б–Є–≤–љ–µ–µ –Ї–∞–ґ–і–∞—П –Є–Ј –љ–Є—Е, —В–µ–Љ –±–Њ–ї—М—И–µ —Б–Є–љ–µ—А–≥–Є—З–µ—Б–Ї–Є–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –≤ –і–∞–љ–љ–Њ–є —В–Њ—З–Ї–Є. –Т –Ї–Њ–љ—Ж–µ –Ї–Њ–љ—Ж–Њ–≤ —А–∞–і–Є–∞–ї—М–љ—Л–є —А–∞–Ј–Љ–µ—А –≤—Б–µ—Е –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –њ—А–Є –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–Є —Г–Љ–љ–Њ–ґ–∞–µ—В—Б—П –љ–∞ —Н—В–Њ—В –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В. –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –њ–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ –Њ–і–љ–Њ–є –Є —В–Њ–є –ґ–µ –љ–Њ—В–µ –Є –Ј–≤—Г—З–∞—Й–Є–µ —Б—А–∞–Ј—Г –≤ –љ–µ—Б–Ї–Њ–ї—М–Ї–Є—Е –Њ–Ї—В–∞–≤–∞—Е, –њ—А–Є –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–Є –±—Г–і—Г—В —Б–Є–ї—М–љ–Њ –≤—Л–і–µ–ї—П—В—М—Б—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –±–ї–Є–Ј–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї, –Ї–Њ—В–Њ—А—Л–µ –Ј–≤—Г—З–∞—В —В–Њ–ї—М–Ї–Њ –≤ –Њ–і–љ–Њ–є –Њ–Ї—В–∞–≤–µ. –≠—В–∞ —Д–Є—И–Ї–∞ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є—П –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –Њ–њ—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–є (–≤–Ї–ї—О—З–∞–µ–Љ–Њ–є/–≤—Л–Ї–ї—О—З–µ–Љ–Њ–є) –Є –≤–Ї–ї–∞–і –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є –Є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –≤–Ї–ї–∞–і–∞ –Њ—В —З–∞—Б—В–Њ—В—Л, –Є –≤–Њ–Њ–±—Й–µ –≤–Ї–ї–∞–і —Б–Є–љ–µ—А–≥–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ –≤ –Њ–±—Й—Г—О –Ї–∞—А—В–Є–љ—Г –і–Њ–ї–ґ–µ–љ —В—Й–∞—В–µ–ї—М–љ–Њ –њ–Њ–і–±–Є—А–∞—В—М—Б—П –≤–µ—Б–Њ–≤—Л–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є, –Є–љ–∞—З–µ —Н—В–∞ —Д–Є—И–Ї–∞ –њ—А–Є–љ–µ—Б—С—В –±–Њ–ї—М—И–µ –љ–µ—А–∞–Ј–±–µ—А–Є—Е–Є, –љ–µ–ґ–µ–ї–Є –њ–Њ–ї—М–Ј—Л.
–Ъ–∞—Б–∞—В–µ–ї—М–љ–Њ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є —Ж–≤–µ—В–∞ –ї–µ–њ–µ—Б—В–Ї–∞ –Њ—В —З–∞—Б—В–Њ—В—Л: –Њ—З–µ–≤–Є–і–љ–Њ –і–Њ–ї–ґ–љ—Л –±—Л—В—М –Ї–∞–Ї–Є–µ-–ї–Є–±–Њ —Д–Њ—А–Љ—Г–ї—Л –Є–ї–Є –Ї—А–Є–≤—Л–µ, –≤—Л–њ–Њ–ї–љ—П—О—Й–Є–µ —Д—Г–љ–Ї—Ж–Є—О —Б–Њ–њ–Њ—Б—В–∞–≤–ї–µ–љ–Є—П RGB- –Є–ї–Є HSB-–Ј–љ–∞—З–µ–љ–Є–є —З–∞—Б—В–Њ—В–µ. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ HSB —В—Г—В –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ —Г–і–Њ–±–љ–µ–µ: –Љ–Њ–ґ–љ–Њ –њ—А–Є–≤—П–Ј–∞—В—М H-–Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Г –Ї —З–∞—Б—В–Њ—В–µ. –Э–Њ –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ, –љ—Г–ґ–љ–Њ —В—Й–∞—В–µ–ї—М–љ–Њ –њ–Њ–Є–Ј—Г—З–∞—В—М —Ж–≤–µ—В–Њ–≤—Л–µ –Љ–Њ–і–µ–ї–Є, –Љ–Њ–і–µ–ї–Є —Б–Љ–µ—И–µ–љ–Є—П —Ж–≤–µ—В–Њ–≤ –Є –≤—Л–±—А–∞—В—М –Њ–њ—В–Є–Љ–∞–ї—М–љ—Л–є –≤–∞—А–Є–∞–љ—В: –Њ–њ—В–Є–Љ–∞–ї—М–љ—Л–є вАФ –Ј–љ–∞—З–Є—В —В–∞–Ї–Њ–є, —З—В–Њ–±—Л –њ–Њ–ї—Г—З–∞—В—М –±–µ–ї—Л–є —Ж–≤–µ—В –Є–Љ–µ–љ–љ–Њ —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ —Н—В–Њ –љ—Г–ґ–љ–Њ. –Т–µ—А–Њ—П—В–љ–Њ, –љ—Г–ґ–љ–Њ —Ж–≤–µ—В–∞ –≤ —Ж–≤–µ—В–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –њ—А–µ–і—Б—В–∞–≤–ї—П—В—М –≤–µ–Ї—В–Њ—А–∞–Љ–Є, —Б–Ї–ї–∞–і—Л–≤–∞—В—М —Н—В–Є –≤–µ–Ї—В–Њ—А—Л –∞ –њ–Њ—В–Њ–Љ –љ–Њ—А–Љ–∞–ї–Є–Ј–Њ–≤–∞—В—М —А–µ–Ј—Г–ї—М—В–Є—А—Г—О—Й–Є–є –≤–µ–Ї—В–Њ—А.
–Т —Ж–µ–ї–Њ–Љ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М —З–∞—Б—В–Њ—В—Л –Є —Ж–≤–µ—В–∞ –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –њ—А–Є–Љ–µ—А–љ–Њ —В–∞–Ї–Њ–є, –Ї–∞–Ї–Њ–є —П–≤–ї—П–µ—В—Б—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М —Ж–≤–µ—В–∞ –Њ—В —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –≤ —В–µ–њ–ї–Њ–≤–Є–Ј–Њ—А–∞—Е:

.
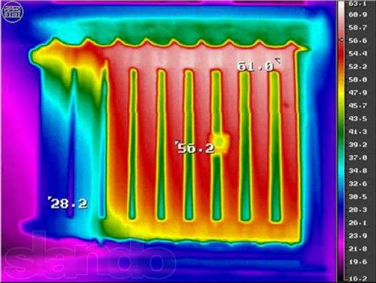
–Ю–і–Є–љ –Є–љ—В–µ—А–µ—Б–љ—Л–є –њ–Њ–±–Њ—З–љ—Л–є —Н—Д—Д–µ–Ї—В –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В–µ–є FFT: —З–∞—Б—В–Њ—В–љ–Њ–µ —А–∞–Ј—А–µ—И–µ–љ–Є–µ –њ–∞–і–∞–µ—В —Б —Г–Љ–µ–љ—М—И–µ–љ–Є–µ–Љ —З–∞—Б—В–Њ—В—Л. –С–ї–∞–≥–Њ–і–∞—А—П —Н—В–Њ–Љ—Г, –ї–µ–њ–µ—Б—В–Ї–Є –љ–µ –±—Г–і—Г—В –њ–Њ–ї–љ–Њ—Б—В—М—О –њ–µ—А–µ–Ї—А—Л–≤–∞—В—М—Б—П: –Э–І-–ї–µ–њ–µ—Б—В–Ї–Є –±—Г–і—Г—В —И–Є—А–µ (–≤ –њ–ї–∞–љ–µ —Г–≥–ї–Њ–≤–Њ–≥–Њ —А–∞–Ј–Љ–µ—А–∞) –Т–І-–ї–µ–њ–µ—Б—В–Ї–Њ–≤. –° —А–Њ—Б—В–Њ–Љ —З–∞—Б—В–Њ—В—Л, –њ—А–Є –њ—А–Њ—З–Є—Е —А–∞–≤–љ—Л—Е, —И–Є—А–Є–љ–∞ –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –±—Г–і–µ—В —Г–Љ–µ–љ—М—И–∞—В—М—Б—П. –Я–Њ—Н—В–Њ–Љ—Г –≤ –ї—О–±—Л—Е —Б–ї—Г—З–∞—П—Е, –±–µ–ї–∞—П —Б–µ—А–і—Ж–µ–≤–Є–љ–∞, –њ–Њ–ї—Г—З–µ–љ–љ–∞—П –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ –Љ–љ–Њ–≥–Њ–Ї—А–∞—В–љ—Л—Е –љ–∞–ї–Њ–ґ–µ–љ–Є–є –ї–µ–њ–µ—Б—В–Ї–Њ–≤, –±—Г–і–µ—В –≤–Є–і–љ–∞ —В–Њ–ї—М–Ї–Њ –≤ —Б–∞–Љ–Њ–Љ —Ж–µ–љ—В—А–µ —Б–Ї–Њ–њ–ї–µ–љ–Є—П –ї–µ–њ–µ—Б—В–Ї–Њ–≤ вАФ –≤–і–Њ–ї—М –Є—Е –Њ—Б–Є, –≤ —В–Њ –≤—А–µ–Љ—П –Ї–∞–Ї –≤–Њ–Ї—А—Г–≥ —Н—В–Њ–є –Њ—Б–Є –±—Г–і–µ—В —Е–Њ—А–Њ—И–Њ –≤–Є–і–љ–∞ –њ–Њ—Б–ї–Њ–є–љ–∞—П —Б—В—А—Г–Ї—В—Г—А–∞ –≤—Б–µ—Е –ї–µ–њ–µ—Б—В–Ї–Њ–≤ (–њ–Њ—Б–Љ–Њ—В—А–Є—В–µ –µ—Й—С —А–∞–Ј –љ–∞ –Љ–Њ–є —Б–∞–Љ–Њ–і–µ–ї—М–љ—Л–є —А–Є—Б—Г–љ–Њ–Ї (—Б–і–µ–ї–∞–љ –≤ —Д–Њ—В–Њ—И–Њ–њ–µ) –≤—Л—И–µ вАФ –Ї—А–∞—Б–љ—Л–є –ї–µ–њ–µ—Б—В–Њ–Ї –љ–∞–Є–±–Њ–ї–µ–µ —И–Є—А–Њ–Ї, —Б–Є–љ–Є–є вАФ –љ–∞–Є–±–Њ–ї–µ–µ —Г–Ј–Њ–Ї).
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Б —Г—З—С—В–Њ–Љ —А–∞–Ј–љ–Є—Ж—Л —И–Є—А–Є–љ—Л –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –Є –Љ–µ—Е–∞–љ–Є–Ј–Љ–Њ–Љ —Б–ї–Њ–ґ–µ–љ–Є—П —Ж–≤–µ—В–∞, –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ –њ–ї–∞–љ–Є—А—Г–µ—В—Б—П –њ—А–Є–Љ–µ—А–љ–Њ —В–∞–Ї–Є–Љ:
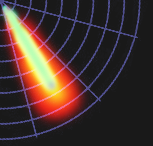 (–Ю–њ—П—В—М –ґ–µ: –Ї–Њ–љ—Ж–µ–њ—В-–∞—А—В –≤ –§–Њ—В–Њ—И–Њ–њ–µ)–І—В–Њ –≤ —Ж–µ–ї–Њ–Љ –і–∞—С—В —В–∞–Ї–Њ–є –њ–Њ–і—Е–Њ–і?
(–Ю–њ—П—В—М –ґ–µ: –Ї–Њ–љ—Ж–µ–њ—В-–∞—А—В –≤ –§–Њ—В–Њ—И–Њ–њ–µ)–І—В–Њ –≤ —Ж–µ–ї–Њ–Љ –і–∞—С—В —В–∞–Ї–Њ–є –њ–Њ–і—Е–Њ–і?–Т–Љ–µ—Б—В–Њ –≥–∞—А–Љ–Њ–љ–Є–Ї –≤—Л –≤–Є–і–Є—В–µ –љ–Њ—В—Л. –Т–Љ–µ—Б—В–Њ –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ вАФ —Г–≥–ї—Л. –Т–Љ–µ—Б—В–Њ –∞–Ї–Ї–Њ—А–і–Њ–≤ вАФ —Д–Є–≥—Г—А—Л –Є–Ј –ї–µ–њ–µ—Б—В–Ї–Њ–≤.
–Э–µ–Љ–љ–Њ–≥–Њ –Њ–± –∞–Ї–Ї–Њ—А–і–∞—Е. –Ъ–∞–Ї —П —Г–ґ–µ –њ–Є—Б–∞–ї –≤—Л—И–µ, –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П –∞–Ї–Ї–Њ—А–і–Њ–≤ –њ–Њ—А–∞–Ј–Є—В –≤–∞—Б —Б–≤–Њ–µ–є –Њ–±—К—С–Љ–љ–Њ—Б—В—М—О. –Ш–Ј –≤—Б–µ–≥–Њ —Н—В–Њ–≥–Њ –±–µ–Ј–Њ–±—А–∞–Ј–Є—П –Љ–Њ–ґ–љ–Њ –≤–Ј—П—В—М –љ–µ–±–Њ–ї—М—И–Њ–є –њ–ї–∞—Б—В —Б–∞–Љ—Л—Е –њ—А–Њ—Б—В—Л—Е –∞–Ї–Ї–Њ—А–і–Њ–≤ вАФ —В—А–µ–Ј–≤—Г—З–Є—П.
–Э–µ –ї—О–±—Л–µ —В—А–Є –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –Ј–≤—Г—З–∞—Й–Є–µ –љ–Њ—В—Л –љ–∞–Ј—Л–≤–∞—О—В—Б—П —В—А–µ–Ј–≤—Г—З–Є—П–Љ–Є, –∞ —В–Њ–ї—М–Ї–Њ —В–µ, –Ї–Њ—В–Њ—А—Л–µ —Б–Њ—Б—В–Њ—П—В –Є–Ј —В—А—С—Е –љ–Њ—В, –Є–љ—В–µ—А–≤–∞–ї—Л –Љ–µ–ґ–і—Г –Ї–Њ—В–Њ—А—Л–Љ–Є (–µ—Б–ї–Є –Њ—В–±—А–Њ—Б–Є—В—М –Њ–і–Є–љ –Љ–Њ–Љ–µ–љ—В –Њ –Ї–Њ—В–Њ—А–Њ–Љ вАФ –њ–∞—А—Г –∞–±–Ј–∞—Ж–µ–≤ –љ–Є–ґ–µ) –Љ–µ–ґ–і—Г –Ї–Њ—В–Њ—А—Л–Љ–Є —П–≤–ї—П—О—В—Б—П —В–µ—А—Ж–Є—П–Љ–Є. –Т–Њ–Њ–±—Й–µ-—В–Њ –љ–µ—В —В–∞–Ї–Њ–≥–Њ –Є–љ—В–µ—А–≤–∞–ї–∞ –Ї–∞–Ї ¬Ђ—В–µ—А—Ж–Є—П¬ї, –∞ –µ—Б—В—М –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–µ–є
—В–µ—А—Ж–Є–Є. –Э–∞—Б –ґ–µ –Є–љ—В–µ—А–µ—Б—Г—О—В –Љ–∞–ї–∞—П —В–µ—А—Ж–Є—П вАФ –Є–љ—В–µ—А–≤–∞–ї –≤ —В—А–Є –њ–Њ–ї—Г—В–Њ–љ–∞, –Є –±–Њ–ї—М—И–∞—П —В–µ—А—Ж–Є—П вАФ –Є–љ—В–µ—А–≤–∞–ї –≤ —З–µ—В—Л—А–µ –њ–Њ–ї—Г—В–Њ–љ–∞.
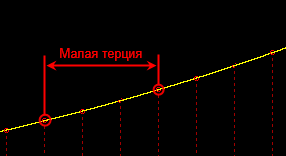
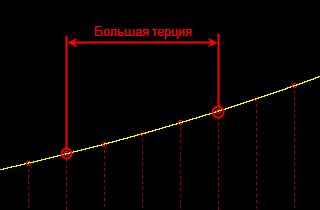
–Э–∞–њ–Њ–Љ–љ—О –µ—Й—С —А–∞–Ј, —З—В–Њ —Н—В–Њ –Є–љ—В–µ—А–≤–∞–ї –Љ–µ–ґ–і—Г
–ї—О–±—Л–Љ–Є –і–≤—Г–Љ—П –љ–Њ—В–∞–Љ–Є, –љ–µ –≤–∞–ґ–љ–Њ вАФ –Ї–∞–Ї–Є–Љ–Є. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Љ—Л —Г—Б–ї–Њ–≤–Є–ї–Є—Б—М –і–µ–ї–Є—В—М –Њ–Ї—В–∞–≤—Г –љ–∞ 12 —А–∞–≤–љ—Л—Е –Є–љ—В–µ—А–≤–∞–ї—М–љ—Л—Е —З–∞—Б—В–µ–є, –Ї–Њ—В–Њ—А—Л–µ –Љ—Л –љ–∞–Ј—Л–≤–∞–µ–Љ –њ–Њ–ї—Г—В–Њ–љ–∞–Љ–Є, –љ–µ –Є–≥—А–∞–µ—В —А–Њ–ї–Є, –Ї–∞–Ї–Є–µ –∞–±—Б–Њ–ї—О—В–љ—Л –Ј–љ–∞—З–µ–љ–Є—П –Є–Љ–µ—О—В —З–∞—Б—В–Њ—В—Л –±–∞–Ј–Њ–≤—Л—Е —В–Њ–љ–Њ–≤ –і–≤—Г—Е —Б—А–∞–≤–љ–Є–≤–∞–µ–Љ—Л—Е –љ–Њ—В. –Ш–≥—А–∞–µ—В —А–Њ–ї—М —В–Њ–ї—М–Ї–Њ –Є—Е –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ–ї—Г—В–Њ–љ вАФ —Н—В–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ 1 : 2
1/12, –Љ–∞–ї–∞—П —В–µ—А—Ж–Є—П вАФ —Н—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ 1 : 2
3/12, –∞ –±–Њ–ї—М—И–∞—П —В–µ—А—Ж–Є—П вАФ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ 1 : 2
4/12.
¬Ђ–Т –ї—Г—З—И–Є—Е —В—А–∞–і–Є—Ж–Є—П—Е¬ї –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–Є, –Є–Љ–µ—П –і–≤–∞ –≤–∞—А–Є–∞–љ—В–∞ —В–µ—А—Ж–Є–Є, –Љ—Л –њ–Њ–ї—Г—З–∞–µ–Љ 4 –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Є –Є–Ј —Н—В–Є—Е –і–≤—Г—Е –Є–љ—В–µ—А–≤–∞–ї–Њ–≤:
- –С–Њ–ї—М—И–∞—П —В–µ—А—Ж–Є—П + –Љ–∞–ї–∞—П —В–µ—А—Ж–Є—П = –Ь–∞–ґ–Њ—А–љ–Њ–µ —В—А–µ–Ј–≤—Г—З–Є–µ:
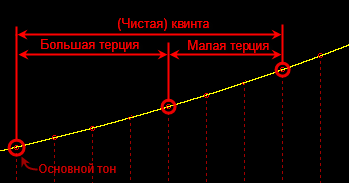
- –Ь–∞–ї–∞—П —В–µ—А—Ж–Є—П + –±–Њ–ї—М—И–∞—П —В–µ—А—Ж–Є—П = –Ь–Є–љ–Њ—А–љ–Њ–µ —В—А–µ–Ј–≤—Г—З–Є–µ:
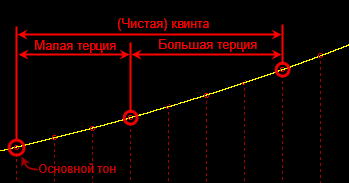
- –С–Њ–ї—М—И–∞—П —В–µ—А—Ж–Є—П + –±–Њ–ї—М—И–∞—П —В–µ—А—Ж–Є—П = –£–≤–µ–ї–Є—З–µ–љ–љ–Њ–µ —В—А–µ–Ј–≤—Г—З–Є–µ
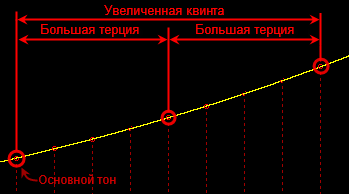
- –Ь–∞–ї–∞—П —В–µ—А—Ж–Є—П + –Ь–∞–ї–∞—П —В–µ—А—Ж–Є—П = –£–Љ–µ–љ—М—И–µ–љ–љ–Њ–µ —В—А–µ–Ј–≤—Г—З–Є–µ
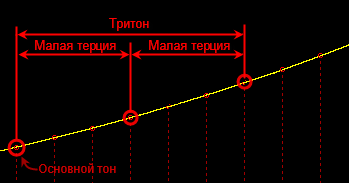
–Я—А–Є—З—С–Љ –њ–µ—А–≤—Л–µ –і–≤–∞ –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ —З–∞—Й–µ, —З–µ–Љ –≤—В–Њ—А—Л–µ –і–≤–∞, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –њ–µ—А–≤—Л–µ –і–≤–∞ —Б—З–Є—В–∞—О—В—Б—П –Ї–Њ–љ—Б–Њ–љ–Є—А—Г—О—Й–Є–Љ–Є (–±–ї–∞–≥–Њ–Ј–≤—Г—З–љ—Л–Љ–Є), –∞ –≤—В–Њ—А—Л–µ –і–≤–∞ вАФ –і–Є—Б—Б–Њ–љ–Є—А—Г—О—Й–Є–Љ–Є (—В.–µ. –љ–µ–±–ї–∞–≥–Њ–Ј–≤—Г—З–љ—Л–Љ–Є, –≤—Л–Ј—Л–≤–∞—О—Й–Є–Љ–Є –Њ—Й—Г—Й–µ–љ–Є–µ –і–Є—Б—Б–Њ–љ–∞–љ—Б–∞). –≠—В–Њ —Б–≤–Њ–є—Б—В–≤–Њ –њ–Њ—Б–ї–µ–і–љ–Є—Е –і–≤—Г—Е —З–∞—Б—В–Њ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П —З—В–Њ–±—Л —Б–Њ–Ј–і–∞—В—М –Љ–Њ–Љ–µ–љ—В –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ—Б—В–Є –≤ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–Є.
–°—З–Є—В–∞–µ—В—Б—П, —З—В–Њ –Љ–∞–ґ–Њ—А–љ–Њ–µ —В—А–µ–Ј–≤—Г—З–Є–µ –Ј–≤—Г—З–Є—В —А–∞–і–Њ—Б—В–љ–Њ, –∞ –Љ–Є–љ–Њ—А–љ–Њ–µ вАФ –≥—А—Г—Б—В–љ–Њ. –Ф–∞–ґ–µ —Б–ї–Њ–≤–∞ ¬Ђ–Љ–∞–ґ–Њ—А–љ—Л–є¬ї –Є ¬Ђ–Љ–Є–љ–Њ—А–љ—Л–є¬ї, –Ї–∞–Ї —П –њ–Њ–≥–ї—П–ґ—Г, —Б—В–∞–ї–Є —Б–Є–љ–Њ–љ–Є–Љ–∞–Љ–Є —Б–ї–Њ–≤ ¬Ђ—А–∞–і–Њ—Б—В–љ—Л–є¬ї –Є ¬Ђ–≥—А—Г—Б—В–љ—Л–є¬ї. –•–Њ—В—П –љ–∞ —Б–∞–Љ–Њ–Љ –ґ–µ –і–µ–ї–µ —Н—В–Њ –њ—А–Њ—Б—В–Њ –ї–∞—В–Є–љ—Б–Ї–Є–µ —Б–ї–Њ–≤–∞ major –Є minor, –њ–µ—А–µ–≤–Њ–і—П—Й–Є–µ—Б—П –Ї–∞–Ї ¬Ђ–±–Њ–ї—М—И–Є–є¬ї –Є ¬Ђ–Љ–µ–љ—М—И–Є–є¬ї —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, –Є –Њ–љ–Є –њ—А–Њ—Б—В–Њ –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—В, —Б –Ї–∞–Ї–Њ–є —В–µ—А—Ж–Є–Є (–±–Њ–ї—М—И–Њ–є –Є–ї–Є –Љ–∞–ї–Њ–є) –љ–∞—З–Є–љ–∞–µ—В—Б—П –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ —В—А–µ–Ј–≤—Г—З–Є—П. –І—В–Њ –ґ–µ –Ї–∞—Б–∞–µ—В—Б—П —А–∞–і–Њ—Б—В–љ–Њ–≥–Њ –Є –≥—А—Г—Б—В–љ–Њ–≥–Њ –Ј–≤—Г—З–∞–љ–Є—П, —В–Њ –Љ–Њ–ґ–љ–Њ —А–∞–і–Њ—Б—В–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –њ–Њ—Б—В—А–Њ–Є—В—М –Є–Ј –њ–Њ–і–∞–≤–ї—П—О—Й–µ–≥–Њ –±–Њ–ї—М—И–Є–љ—Б—В–≤–∞ –Љ–Є–љ–Њ—А–љ—Л—Е –∞–Ї–Ї–Њ—А–і–Њ–≤, –Є –љ–∞–Њ–±–Њ—А–Њ—В, —В–∞–Ї —З—В–Њ –µ—Б–ї–Є –Є –≥–Њ–≤–Њ—А–Є—В –Њ–± —Н–Љ–Њ—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–є –Њ–Ї—А–∞—Б–Ї–µ –∞–Ї–Ї–Њ—А–і–∞, —В–Њ —Н—В–Њ ¬Ђ–Њ–Ї—А–∞—Б–Ї–∞ –≤ –≤–∞–Ї—Г—Г–Љ–µ¬ї.
–Р–Ї–Ї–Њ—А–і–∞–Љ –і–∞—О—В –љ–∞–Ј–≤–∞–љ–Є–µ –≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–Є —Б –љ–∞–Ј–≤–∞–љ–Є–µ–Љ –љ–Њ—В—Л, –Ї–Њ—В–Њ—А–∞—П –њ–Њ—Б–ї—Г–ґ–Є–ї–∞ –±–∞–Ј–Њ–≤–Њ–є –і–ї—П –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –∞–Ї–Ї–Њ—А–і–∞ (–Њ—В –Ї–Њ—В–Њ—А–Њ–є –±—Л–ї–∞ –Њ—В–ї–Њ–ґ–µ–љ–∞ —Б–љ–∞—З–∞–ї–∞ –Њ–і–љ–∞ —В–µ—А—Ж–Є—П, –∞ –Ј–∞—В–µ–Љ –µ—Й—С –Њ–і–љ–∞). –Э–∞–њ—А–Є–Љ–µ—А: –Ф–Њ-–Љ–Є–љ–Њ—А –Є–ї–Є –§–∞-–Љ–∞–ґ–Њ—А. –Т –ї–∞—В–Є–љ—Б–Ї–Њ–є –ґ–µ —Б–Є—Б—В–µ–Љ–µ –Љ–∞–ґ–Њ—А–љ—Л–µ –∞–Ї–Ї–Њ—А–і—Л –Њ–±–Њ–Ј–љ–∞—З–∞—О—В—Б—П —В–Њ–є –ґ–µ –±—Г–Ї–≤–Њ–є, —З—В–Њ –Є –Њ—Б–љ–Њ–≤–љ–Њ–є —В–Њ–љ, –∞ –Љ–Є–љ–Њ—А–љ—Л–µ вАФ –±—Г–Ї–≤–Њ–є –љ–Њ—В—Л, —Б—В–∞–≤—И–µ–є –Њ—Б–љ–Њ–≤–љ—Л–Љ —В–Њ–љ–Њ–Љ –∞–Ї–Ї–Њ—А–і–∞, —Б –і–Њ–±–∞–≤–ї–µ–љ–Є–µ–Љ —Б—В—А–Њ—З–љ–Њ–є –±—Г–Ї–≤—Л ¬Ђm¬ї. –Э–∞–њ—А–Є–Љ–µ—А
Cm –Є
F.
–Ґ–µ–њ–µ—А—М –≤–µ—А–љ—С–Љ—Б—П –Ї –њ–Њ–ї—П—А–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В. –Ґ–µ—А—Ж–Є–Є –њ—А–µ–Њ–±—А–∞–Ј—Г—О—В—Б—П –≤ —Г–≥–ї—Л:
–Ь–∞–ї–∞—П —В–µ—А—Ж–Є—П вАФ –њ—А—П–Љ–Њ–є —Г–≥–Њ–ї (90¬∞).
–С–Њ–ї—М—И–∞—П —В–µ—А—Ж–Є—П вАФ —Г–≥–Њ–ї 120 ¬∞.
–Ґ—А–µ–Ј–≤—Г—З–Є—П–Љ, –≤ —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, –±—Г–і—Г—В —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Њ–≤–∞—В—М –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Є –Є–Ј –ї–µ–њ–µ—Б—В–Ї–Њ–≤:
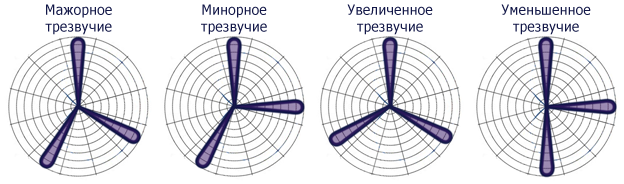
–Т–∞–ґ–љ—Л–µ —Б–≤–Њ–є—Б—В–≤–∞:
- –Ю—В –Ї–∞–Ї–Њ–є –±—Л –љ–Њ—В—Л –љ–Є –±—Л–ї –њ–Њ—Б—В—А–Њ–µ–љ –∞–Ї–Ї–Њ—А–і, –Њ–љ –≤—Б–µ–≥–і–∞ —Б–Њ—Е—А–∞–љ—П–µ—В —Б–≤–Њ—О –Ї–Њ–љ—Д–Є–≥—Г—А–∞—Ж–Є—О –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –Є –њ—А–Є —Б–Љ–µ–љ–µ –Њ—Б–љ–Њ–≤–љ–Њ–≥–Њ —В–Њ–љ–∞ –∞–Ї–Ї–Њ—А–і–∞ –њ—А–Њ–Є—Б—Е–Њ–і–Є—В —В–Њ–ї—М–Ї–Њ –≤—А–∞—Й–µ–љ–Є–µ —В—А—С—Е–ї–µ–њ–µ—Б—В–Ї–Њ–≤–Њ–≥–Њ –±–ї–Њ–Ї–∞ –≤–Њ–Ї—А—Г–≥ —Ж–µ–љ—В—А–∞. –£–≥–ї—Л —Б–Њ—Е—А–∞–љ—П—О—В—Б—П.
- –Х—Б–ї–Є –Ї–∞–Ї–Є–µ-—В–Њ –љ–Њ—В—Л (–Є–ї–Є –≤—Б–µ –љ–Њ—В—Л) –∞–Ї–Ї–Њ—А–і–∞ –±—Г–і—Г—В –њ—А–Њ–і—Г–±–ї–Є—А–Њ–≤–∞–љ—Л –≤ –і—А—Г–≥–Є—Е –Њ–Ї—В–∞–≤–∞—Е, —Н—В–Њ –љ–µ –Є—Б–Ї–∞–Ј–Є—В –≤–Є–Ј—Г–∞–ї–Є–Ј–∞—Ж–Є—О –∞–Ї–Ї–Њ—А–і–∞.
–Ґ–µ–њ–µ—А—М –Ї–Њ–µ-—З—В–Њ –Њ–± –∞–Ї–Ї–Њ—А–і–∞—Е, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –љ–µ-—Б–њ–µ—Ж–Є–∞–ї–Є—Б—В—Л –љ–µ –Ј–љ–∞—О—В.
–Х—Б—В—М —В–∞–Ї–Њ–µ —П–≤–ї–µ–љ–Є–µ (–Є –њ–Њ–љ—П—В–Є–µ) –Ї–∞–Ї
–Њ–±—А–∞—Й–µ–љ–Є—П –∞–Ї–Ї–Њ—А–і–Њ–≤.
- –Т—Л –Љ–Њ–ґ–µ—В–µ —Б–∞–Љ—Г—О –љ–Є–Ј–Ї—Г—О –љ–Њ—В—Г –∞–Ї–Ї–Њ—А–і–∞ –њ–µ—А–µ–љ–µ—Б—В–Є –љ–∞ –Њ–Ї—В–∞–≤—Г –≤–≤–µ—А—Е.
- –Ш–ї–Є —Б–∞–Љ—Г—О –≤–µ—А—Е–љ—О—О –љ–Њ—В—Г –∞–Ї–Ї–Њ—А–і–∞ –њ–µ—А–µ–љ–µ—Б—В–Є –љ–∞ –Њ–Ї—В–∞–≤—Г –≤–љ–Є–Ј.
–≠—В–∞ –Љ–∞–љ–Є–њ—Г–ї—П—Ж–Є—П –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–Њ–і–µ–ї–∞–љ—Л –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —А–∞–Ј. –Ъ–ї—О—З–µ–≤–Њ–є –Љ–Њ–Љ–µ–љ—В –Њ–±—А–∞—Й–µ–љ–Є–є: –Њ–±—А–∞—Й–µ–љ–Є—П –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –Љ–µ–љ—П—О—В –Ј–≤—Г—З–∞–љ–Є—П, –љ–Њ –Њ–љ–Є –љ–µ –Љ–µ–љ—П—О—В –∞–Ї–Ї–Њ—А–і–∞ –Є –µ–≥–Њ –љ–∞–Ј–≤–∞–љ–Є—П –њ–Њ —Б—Г—В–Є (–†–µ-–Љ–Є–љ–Њ—А –Њ—Б—В–∞–љ–µ—В—Б—П —А–µ-–Љ–Є–љ–Њ—А–Њ–Љ).
–Ґ—А–Є –њ–Њ–і—А—П–і –≤—Л–њ–Њ–ї–љ–µ–љ–љ—Л—Е –Њ–±—А–∞—Й–µ–љ–Є—П –і–∞—О—В –Є–Ј–љ–∞—З–∞–ї—М–љ—Л–є –∞–Ї–Ї–Њ—А–і, –љ–Њ –њ–µ—А–µ–љ–µ—Б—С–љ–љ—Л–є –љ–∞ –Њ–Ї—В–∞–≤—Г –≤–љ–Є–Ј –Є–ї–Є –љ–∞ –Њ–Ї—В–∞–≤—Г –≤–≤–µ—А—Е.
–Ю–±—А–∞—Й–µ–љ–Є—П –∞–Ї–Ї–Њ—А–і–∞ ¬Ђ–Ф–Њ-–Љ–Є–љ–Њ—А¬ї –љ–∞ –њ—А–Є–Љ–µ—А–µ —Б–µ—В–Ї–Є –њ–Њ–ї—Г—В–Њ–љ–Њ–≤ –Є –Ї–ї–∞–≤–Є–∞—В—Г—А—Л:
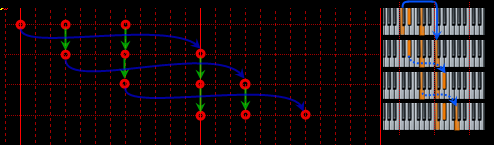
–Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ, –љ–Њ –Ј–µ—А–Ї–∞–ї—М–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –Њ—Б—Г—Й–µ—Б—В–≤–ї—П–µ—В—Б—П –Њ–±—А–∞—Й–µ–љ–Є–µ –≤–љ–Є–Ј.
–Ю–±—А–∞—Й–µ–љ–Є–µ –≤ –љ–µ–Ї–Њ—В–Њ—А–Њ–є —Б—В–µ–њ–µ–љ–Є –Љ–µ–љ—П–µ—В —Е–∞—А–∞–Ї—В–µ—А –Ј–≤—Г—З–∞–љ–Є—П, –љ–Њ –љ–Є–Ї–Њ–≥–і–∞ –љ–µ –і–µ–ї–∞–µ—В –Є–Ј –Љ–∞–ґ–Њ—А–∞ –Љ–Є–љ–Њ—А, –Є–Ј –Љ–Є–љ–Њ—А–∞ вАФ –Љ–∞–ґ–Њ—А –Є–ї–Є –Ї–∞–Ї–Є–µ-–ї–Є–±–Њ –њ–Њ–і–Њ–±–љ—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П. –Р–Ї–Ї–Њ—А–і –Њ—Б—В–∞—С—В—Б—П –њ—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–Њ —В–µ–Љ –ґ–µ, —З–µ–Љ –Њ–љ –±—Л–ї.
–Т–∞–ґ–љ–Њ–µ —Б–≤–Њ–є—Б—В–≤–Њ –∞–Ї–Ї–Њ—А–і–Њ–≤ –≤ –Њ—В–љ–Њ—И–µ–љ–Є–Є –њ–Њ–ї—П—А–љ–Њ–≥–Њ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є—П —Б–њ–µ–Ї—В—А–∞: –≤—Б–µ –Њ–±—А–∞—Й–µ–љ–Є—П –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –∞–Ї–Ї–Њ—А–і–∞ –Є–Љ–µ—О—В –Є–і–µ–љ—В–Є—З–љ—Г—О –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї—Г—О —Д–Њ—А–Љ—Г (–Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—О —Г–≥–ї–Њ–≤ –Љ–µ–ґ–і—Г –ї–µ–њ–µ—Б—В–Ї–∞–Љ–Є). –Я—А–Є –Њ–±—А–∞—Й–µ–љ–Є–Є –∞–Ї–Ї–Њ—А–і–Њ–≤ –ї–µ–њ–µ—Б—В–Ї–Є –љ–µ –і–≤–Є–≥–∞—О—В—Б—П, —Г–≥–ї—Л –љ–µ –Љ–µ–љ—П—О—В—Б—П,, –љ–Њ –Љ–µ–љ—П–µ—В—Б—П —Ж–≤–µ—В –ї–µ–њ–µ—Б—В–Ї–Њ–≤.–Ґ–µ–њ–µ—А—М –љ–µ–Љ–љ–Њ–≥–Њ –њ—А–∞–Ї—В–Є–Ї–Є:
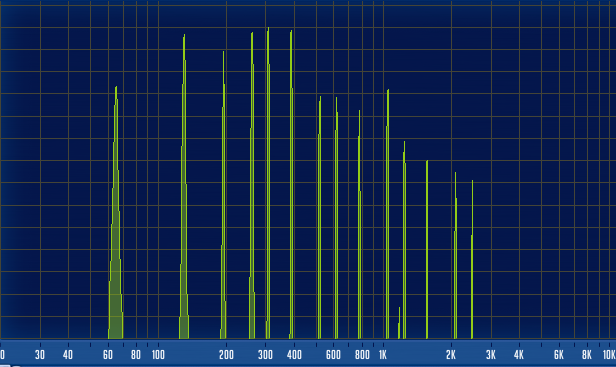
–Ъ–∞–Ї–Є–µ –љ–Њ—В—Л –Ј–і–µ—Б—М –Є–≥—А–∞—О—В? –Х—Б–ї–Є –Њ—В–±—А–Њ—Б–Є—В—М –Њ–Ї—В–∞–≤–љ–Њ–µ –і—Г–±–ї–Є—А–Њ–≤–∞–љ–Є–µ, —Б–Ї–Њ–ї—М–Ї–Њ –љ–Њ—В –Ј–і–µ—Б—М –Є–≥—А–∞–µ—В –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ? –Х—Б–ї–Є —В–∞–Љ –∞–Ї–Ї–Њ—А–і, —В–Њ –Ї–∞–Ї–Њ–є?
–£–≤–µ—А–µ–љ, –±—Л—Б—В—А—Л–Љ –≤–Ј–≥–ї—П–і–Њ–Љ, –≥–ї—П–і—П –љ–∞ —Б–њ–µ–Ї—В—А, –љ–µ–ї—М–Ј—П –і–∞—В—М –Њ—В–≤–µ—В—Л –љ–∞ —Н—В–Є –≤–Њ–њ—А–Њ—Б—Л: –≥–Њ—А–∞–Ј–і–Њ –њ—А–Њ—Й–µ –±—Г–і–µ—В –њ–Њ–ї–Њ–ґ–Є—В—М—Б—П –љ–∞ —Б–ї—Г—Е, –љ–µ–ґ–µ–ї–Є –љ–∞ –Ї–∞—А—В–Є–љ–Ї—Г.
–Э–Њ —Б –њ–Њ–ї—П—А–љ—Л–Љ —Б–њ–µ–Ї—В—А–Њ–∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–Њ–Љ –Љ—Л —Г–≤–Є–і–Є–Љ, —З—В–Њ —Н—В–Њ –∞–Ї–Ї–Њ—А–і ¬Ђ–Ф–Њ-–Љ–Є–љ–Њ—А¬ї, –њ—А–µ—В–µ—А–њ–µ–≤—И–Є–є –Њ–і–љ–Њ –Њ–±—А–∞—Й–µ–љ–Є–µ –≤–љ–Є–Ј, –њ–ї—О—Б —Б—Л–≥—А–∞–љ–љ–∞—П –≤ –±–∞—Б—Г –љ–Њ—В–∞ ¬Ђ–Ф–Њ¬ї:
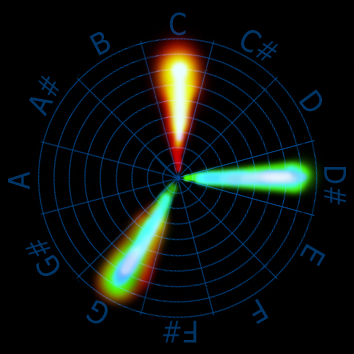 (–≠—В–Њ –≤—Б–µ–≥–Њ –ї–Є—И—М –љ–µ–≤–∞–ґ–љ–Њ –њ–Њ–ї—Г—З–Є–≤—И–Є–є—Б—П –љ–∞–±—А–Њ—Б–Њ–Ї –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ–Љ–Њ–≥–Њ –≤–Є–і–∞: —А–µ–Ј–Ї–Њ—Б—В—М –≥—А–∞–љ–Є—Ж –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–ї–ґ–љ–∞ –±—Л—В—М —В–∞–Ї–Њ–є –Љ—Г—В–љ–Њ–є вАФ —Н—В–Њ –≤—Б—С –Ї–∞–Ї –Љ–Є–љ–Є–Љ—Г–Љ ¬Ђ–њ–Њ–і –≤–Њ–њ—А–Њ—Б–Њ–Љ¬ї, –∞ –Ї–∞–Ї –Љ–∞–Ї—Б–Є–Љ—Г–Љ вАФ –і–Њ–ї–ґ–љ–Њ –ї–µ–≥–Ї–Њ —В–≤–Є–Ї–∞—В—М—Б—П –љ–∞—Б—В—А–Њ–є–Ї–Њ–є —Б–њ–µ–Ї—В—А–Њ–∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–∞).
(–≠—В–Њ –≤—Б–µ–≥–Њ –ї–Є—И—М –љ–µ–≤–∞–ґ–љ–Њ –њ–Њ–ї—Г—З–Є–≤—И–Є–є—Б—П –љ–∞–±—А–Њ—Б–Њ–Ї –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ–Љ–Њ–≥–Њ –≤–Є–і–∞: —А–µ–Ј–Ї–Њ—Б—В—М –≥—А–∞–љ–Є—Ж –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–ї–ґ–љ–∞ –±—Л—В—М —В–∞–Ї–Њ–є –Љ—Г—В–љ–Њ–є вАФ —Н—В–Њ –≤—Б—С –Ї–∞–Ї –Љ–Є–љ–Є–Љ—Г–Љ ¬Ђ–њ–Њ–і –≤–Њ–њ—А–Њ—Б–Њ–Љ¬ї, –∞ –Ї–∞–Ї –Љ–∞–Ї—Б–Є–Љ—Г–Љ вАФ –і–Њ–ї–ґ–љ–Њ –ї–µ–≥–Ї–Њ —В–≤–Є–Ї–∞—В—М—Б—П –љ–∞—Б—В—А–Њ–є–Ї–Њ–є —Б–њ–µ–Ї—В—А–Њ–∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–∞).–Я–Њ–і—Л—В–Њ–ґ—Г –љ–µ–Ї–Њ—В–Њ—А—Л–µ –Ї–ї—О—З–µ–≤—Л–µ –Љ–Њ–Љ–µ–љ—В—Л –Є —В—А–µ–±–Њ–≤–∞–љ–Є—П –Ї –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–Љ—Г –Љ–Њ–µ–є –Ї–Њ–љ—Ж–µ–њ—Ж–Є–Є:
- –Я–Њ–ї—П—А–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–Љ–µ—Б—В–Њ –і–µ–Ї–∞—А—В–Њ–≤—Л—Е. –Р –≤–Њ–Њ–±—Й–µ-—В–Њ –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А –і–Њ–ї–ґ–µ–љ –Є–Љ–µ—В—М –њ–µ—А–µ–Ї–ї—О—З–∞—В–µ–ї—М –і–ї—П –≤—Л–±–Њ—А–∞ –Љ–µ–ґ–і—Г –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–є –Є –њ–Њ–ї—П—А–љ–Њ–є —Б–Є—Б—В–µ–Љ–∞–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В.
- –°–њ–µ–Ї—В—А–∞–ї—М–љ—Л–µ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –і–Њ–ї–ґ–љ—Л –Њ—В–Њ–±—А–∞–ґ–∞—В—М—Б—П –≤ –≤–Є–і–µ –ї–µ–њ–µ—Б—В–Ї–Њ–≤, –∞ –љ–µ —Б—В–Њ–ї–±—Ж–Њ–≤ –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —А–µ–ґ–Є–Љ–µ –Є —Б–µ–Ї—В–Њ—А–Њ–≤ –≤ –њ–Њ–ї—П—А–љ–Њ–Љ.
- –Т –њ–Њ–ї—П—А–љ–Њ–Љ —А–µ–ґ–Є–Љ–µ: –Њ–і–Є–љ –Њ–±–Њ—А–Њ—В вАФ –Њ–і–љ–∞ –Њ–Ї—В–∞–≤–∞.
- –Ю–±—П–Ј–∞—В–µ–ї—М–љ–Њ–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ —Ж–≤–µ—В–∞ –ї–µ–њ–µ—Б—В–Ї–∞ —З–∞—Б—В–Њ—В–µ, –Ї–Њ—В–Њ—А—Г—О –ї–µ–њ–µ—Б—В–Њ–Ї –Њ—В–Њ–ґ–і–µ—Б—В–≤–ї—П–µ—В.
- –Ю–±—П–Ј–∞—В–µ–ї—М–љ–Њ —Б–ї–Њ–ґ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ —Б–Є–љ—В–µ–Ј–∞ —Ж–≤–µ—В–Њ–≤ –њ—А–Є –љ–∞–ї–Њ–ґ–µ–љ–Є–Є –ї–µ–њ–µ—Б—В–Ї–Њ–≤.
- –Ъ–∞–Ї –≤–∞—А–Є–∞–љ—В —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–є –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –≤ —Б—В–µ—А–µ–Њ-–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Љ–Њ–ґ–µ—В –≤–љ–Њ—Б–Є—В—М –≤–Ї–ї–∞–і –≤ —Ж–≤–µ—В –ї–µ–њ–µ—Б—В–Ї–∞ —В–Њ–ґ–µ.
- –Т–Ї–ї—О—З–∞–µ–Љ—Л–є –њ–Њ –ґ–µ–ї–∞–љ–Є—О –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—П –њ—А–Є–љ—Ж–Є–њ —Б–Є–љ–µ—А–≥–Є–Є –≥–∞—А–Љ–Њ–љ–Є–Ї.
- –Ъ—Г—З–∞ –Ї—А—Г—В–Є–ї–Њ–Ї –і–ї—П —В–≤–Є–Ї–Є–љ–≥–∞ –≤—Б–µ–≥–Њ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є—П.
- –Ь–Њ—Й–љ–∞—П —Б–µ—В–Ї–∞-–Њ–≤–µ—А–ї–µ–є, –і–µ–ї—П—Й–∞—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –љ–∞ —Б–µ–Ї—В–Њ—А–∞-–Є–љ—В–µ—А–≤–∞–ї—Л. –Я–Њ –і–µ—Д–Њ–ї—В—Г —Б–µ–Ї—В–∞ –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –љ–∞—Б—В—А–Њ–µ–љ–∞ –љ–∞ 12-–Є–љ—В–µ—А–≤–∞–ї—М–љ—Л–є —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ—Л–є —Б—В—А–Њ–є —Б –Њ–њ–Њ—А–љ–Њ–є —З–∞—Б—В–Њ—В–Њ–є 440 –У—Ж. –Э–Њ—В—Л –і–Њ–ї–ґ–µ–љ –±—Л—В—М –њ–Њ–і–њ–Є—Б–∞–љ—Л. –Я–Њ –ґ–µ–ї–∞–љ–Є—О –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Љ–Њ–ґ–µ—В –≤—Л–±—А–∞—В—М –ї—О–±–Њ–є –і—А—Г–≥–Њ–є —Б—В—А–Њ–є, –њ–Њ–Љ–µ–љ—П—В—М —З–Є—Б–ї–Њ –Є–љ—В–µ—А–≤–∞–ї–Њ–≤, —Б–Љ–µ–љ–Є—В—М —Б—В–Є–ї—М –њ–Њ–і–њ–Є—Б—Л–≤–∞–љ–Є—П –љ–Њ—В, —Б–Љ–µ–љ–Є—В—М –Њ–њ–Њ—А–љ—Г—О —З–∞—Б—В–Њ—В—Г. –Ъ–Њ–љ—Д–Є–≥—Г—А–Є—А—Г–µ–Љ—Л–µ —Б—Г–±–і–µ–ї–µ–љ–Є—П, –љ–∞–њ—А–Є–Љ–µ—А, –і–ї—П —Ж–µ–љ—В–Њ–≤.
- –Ъ–Њ–љ—Д–Є–≥—Г—А–Є—А—Г–µ–Љ—Л–є –≤—Л–±–Њ—А –Љ–µ–ґ–і—Г –і–Њ—Б—В–Є–ґ–µ–љ–Є–µ–Љ –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–љ–Ю–≥–Њ –Є–ї–Є –і–Њ—Б—В–Є–ґ–µ–љ–Є–µ–Љ –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–≥–Њ —З–∞—Б—В–Њ—В–љ–Њ–≥–Њ —А–∞–Ј—А–µ—И–µ–љ–Є—П.
- –Ю–њ—Ж–Є–Њ–љ–∞–ї—М–љ—Л–є —В–≤–Є–Ї–Є–љ–≥ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ FFT –Є —Б–≥–ї–∞–ґ–Є–≤–∞–љ–Є—П –њ–Њ–ї—Г—З–µ–љ–љ—Л—Е –і–∞–љ–љ—Л—Е.
- –Ь–∞—А–Ї–µ—А—Л-–Ї—Г—А—Б–Њ—А—Л, —Б –њ–Њ–Љ–Њ—Й—М—О –Ї–Њ—В–Њ—А—Л—Е –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Љ–Њ–ґ–µ—В —Б—В–∞–≤–Є—В—М –Љ–µ—В–Ї–Є –Є –і–µ–ї–∞—В—М –Є–Ј–Љ–µ—А–µ–љ–Є—П.
- –Р–љ–∞–ї–Є–Ј–∞—В–Њ—А –і–Њ–ї–ґ–µ–љ –±—Л—В—М –≤—Л–њ–Њ–ї–љ–µ–љ –≤ –≤–Є–і–µ VST, —З—В–Њ–±—Л –±—Л–ї–∞ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –µ–≥–Њ –≤ –ї—О–±–Њ–Љ —Е–Њ—Б—В–µ (DAW)
_______________
–Ъ–Њ–≥–і–∞ —П —Г–≤–Є–і–µ–ї —Н—В—Г —А–µ–∞–ї–Є–Ј–∞—Ж–Є—О, —П –Є—Б–њ—Л—В—Л–≤–∞–ї —Б–Љ–µ—И–∞–љ–љ—Л–µ —З—Г–≤—Б—В–≤–∞. –° –Њ–і–љ–Њ–є —Б—В–Њ—А–Њ–љ—Л –Ї–Њ–Љ—Г-—В–Њ –±—Л–ї–Њ –љ–µ –ї–µ–љ—М –≤–Њ–њ–ї–Њ—В–Є—В—М –≤ –ґ–Є–Ј–љ—М –Љ–Њ—О –Є–і–µ—О (–Љ–љ–µ-—В–Њ –≤—Б—С —А–∞–≤–љ–Њ –љ–µ–Ї–Њ–≥–і–∞), –љ–Њ —Б –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л, –Љ–Њ—О –Є–і–µ—О —Б–Є–ї—М–љ–Њ –Є—Б–Ї–∞–Ј–Є–ї–Є –Є –Њ–±–Њ–ї–≤–∞–љ–Є–ї–Є –Ј–∞–і—Г–Љ–Ї—Г –і–Њ —В–∞–Ї–Њ–≥–Њ —Г—А–Њ–≤–љ—П, —З—В–Њ —В–∞–Ї–Њ–є –љ–µ–њ—А–Є–≤—Л—З–љ—Л–є –≤—Л–≤–Њ–і —Б—В–∞–ї –њ—А–Њ—Б—В–Њ –±–µ—Б–њ–Њ–ї–µ–Ј–љ—Л–Љ –Є –љ–µ–њ—А–Є–≥–Њ–і–љ—Л–Љ –і–ї—П —З–µ–≥–Њ-—В–Њ.
–Ъ–Њ–≥–і–∞ —П –≤–Є–ґ—Г —Б–µ–Ї—В–Њ—А—Л –≤–Љ–µ—Б—В–Њ –≥–ї–∞–і–Ї–Є—Е –ї–µ–њ–µ—Б—В–Ї–Њ–≤ вАФ —Г –Љ–µ–љ—П –Є–Ј –≥–ї–∞–Ј –Є–і—С—В –Ї—А–Њ–≤—М

–Ъ–Њ–≥–і–∞ —П –≤–Є–ґ—Г, —З—В–Њ –љ–µ—В —Б—В–Њ–ї—М –≤–∞–ґ–љ–Њ–≥–Њ –∞–і–і–Є—В–Є–≤–љ–Њ–≥–Њ —Б–ї–Њ–ґ–µ–љ–Є—П —Ж–≤–µ—В–Њ–≤ вАФ –Љ–љ–µ –њ–µ—З–∞–ї—М–љ–Њ.
–Э–Њ —Б–∞–Љ–Њ–µ –≥–ї–∞–≤–љ–Њ–µ: —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ
–љ–µ–њ—А–Є–µ–Љ–ї–µ–Љ–Њ –љ–Є–Ј–Ї–Њ–µ —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–µ —А–∞–Ј—А–µ—И–µ–љ–Є–µ.
–Я—А–µ–і–ї–∞–≥–∞—О —Б—А–∞–≤–љ–Є—В—М.
–Т–Њ—В —Б–Ї—А–Є–љ—И–Њ—В –љ–µ–њ–ї–Њ—Е–Њ–≥–Њ –±–µ—Б–њ–ї–∞—В–љ–Њ–≥–Њ —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–∞ Voxengo SPAN, –∞ –љ–∞ –µ–≥–Њ —Д–Њ–љ–µ –Њ—В–Ї—А—Л–ї TrickSpectrum. –°–њ–µ—А–≤–∞ —П –≤ SPAN'–µ —Б–њ–µ—Ж–Є–∞–ї—М–љ–Њ –≤–Ї–ї—О—З–Є–ї —А–µ–ґ–Є–Љ ¬Ђ–Ј–∞–њ–Њ–Љ–Є–љ–∞—В—М –Љ–∞–Ї—Б–Є–Љ—Г–Љ¬ї, —Б—Г–Ј–Є–ї –і–Є–∞–њ–∞–Ј–Њ–љ –Њ—В–Њ–±—А–∞–ґ–∞–µ–Љ–Њ–≥–Њ –Њ–Ї–љ–∞ –і–Њ –њ—А–Є–Љ–µ—А–љ–Њ –Њ–і–љ–Њ–є –Њ–Ї—В–∞–≤—Л –Є –њ—А–Њ—И—С–ї—Б—П –њ–Њ –≤—Б–µ–Љ –њ–Њ–ї—Г—В–Њ–љ–∞–Љ –Њ–Ї—В–∞–≤—Л –њ–Њ–і—А—П–і, –њ–Њ–і–Њ–≤–∞—П –љ–∞ –≤—Е–Њ–і –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–∞ –љ–Њ—В—Г, —Б–Њ—Б—В–Њ—П—Й—Г—О –Є–Ј –Њ–і–љ–Њ–≥–Њ —В–Њ–ї—М–Ї–Њ —Б–Є–љ—Г—Б–Њ–Є–і–∞–ї—М–љ–Њ–≥–Њ —Б–Є–≥–љ–∞–ї. –Я–Њ–ї—Г—З–Є–ї–∞—Б—М —В—С–Љ–љ–Њ-–Ј–µ–ї—С–љ–∞—П –≥—А–µ–±—С–љ–Ї–∞, –њ–Є–Ї–Є –Ї–Њ—В–Њ—А–Њ–є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В —Б–µ—В–Ї–µ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ —Б—В—А–Њ—П. –Ч–∞—В–µ–Љ —П –≤ –≥—А–∞—Д. —А–µ–і–∞–Ї—В–Њ—А–µ –њ–Њ–і–њ–Є—Б–∞–ї –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –љ–Њ—В—Л.

.
–Я–Њ —Н—В–Њ–Љ—Г —Б–Ї—А–Є–љ—И–Њ—В—Г —Е–Њ—А–Њ—И–Њ –≤–Є–і–љ–Њ, —З—В–Њ –і–ї—П –Ї–∞–ґ–і–Њ–є –љ–Њ—В—Л –≤ —Б–Њ—Б—В–∞–≤–µ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —В–µ–Љ–њ–µ—А–Є—А–Њ–≤–∞–љ–љ–Њ–є –Њ–Ї—В–∞–≤—Л —А–∞–Ј—А–µ—И–∞—О—Й–µ–є —Б–њ–Њ—Б–Њ–±–љ–Њ—Б—В–Є SPAN-–∞ —Е–≤–∞—В–∞–µ—В, —З—В–Њ–±—Л –Њ—В–Њ–±—А–∞–Ј–Є—В—М –љ–Њ—В—Г –Ї–∞–Ї –Њ—В–і–µ–ї—М–љ—Л–є –ї–µ–њ–µ—Б—В–Њ–Ї. –Ь–µ–ґ–і—Г –і–≤—Г–Љ—П —Б–Њ—Б–µ–і–љ–Є–Љ–Є –љ–Њ—В–∞–Љ–Є –Љ–Њ–ґ–љ–Њ –µ—Й—С –љ–µ—З—В–Њ –њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ–Њ–µ —Г–Љ–Њ—Б—В–Є—В—М, –Є —Н—В–Њ –±—Г–і–µ—В –≤–Є–і–љ–Њ –љ–∞ —Б–њ–µ–Ї—В—А–µ.
–Э–∞ –Љ–Њ–Љ–µ–љ—В —Б–љ—П—В–Є—П —Б–Ї—А–Є–љ—И–Њ—В–∞ –Ј–≤—Г—З–Є—В –љ–Њ—В–∞ ¬Ђ–Ф–Њ¬ї, –µ—С –≤–Є–і–љ–Њ –љ–∞ —Б–њ–µ–Ї—В—А–µ –Ї–∞–Ї —П—А–Ї–Њ-–Ј–µ–ї—С–љ—Л–є –ї–µ–њ–µ—Б—В–Њ–Ї, –Ї–Њ—В–Њ—А—Л–є –љ–µ –Ј–∞–ї–∞–Ј–Є—В –љ–∞ —Б–Њ—Б–µ–і–љ–Є–µ –љ–Њ—В—Л. –ѓ –Љ–Њ–≥—Г –ї–µ–≥–Ї–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М, –љ–µ —А–∞—Б—Б—В—А–Њ–µ–љ–∞ –ї–Є —Б–ї—Г—З–∞–є–љ–Њ –љ–Њ—В–∞ ¬Ђ–Ф–Њ¬ї –љ–∞ 30 —Ж–µ–љ—В–Њ–≤ –≤–љ–Є–Ј –Є–ї–Є –≤–≤–µ—А—Е. –†–∞–Ј—А–µ—И–µ–љ–Є—П –Є –Љ–µ—В–Њ–і –≤–Є–Ј—Г–∞–ї–Є–Ј–∞—Ж–Є–Є –њ–Њ–Ј–≤–Њ–ї—П–µ—В.
–Х—Б–ї–Є –ґ–µ –њ–Њ—Б–Љ–Њ—В—А–µ—В—М –љ–∞ TrickSpectrum, —В–Њ –≤–Є–і–љ–Њ, —З—В–Њ –∞–±—Б–Њ–ї—О—В–љ–Њ —В–∞ –ґ–µ –љ–Њ—В–∞ –Њ—В–Њ–±—А–∞–ґ–∞–µ—В—Б—П –Ї–∞–Ї –љ–µ—З—В–Њ —А–∞–≤–љ–Њ–µ, –Є –Ј–∞–љ–Є–Љ–∞–µ—В (–љ–∞–±–µ—А–Є—В–µ –≤–Њ–Ј–і—Г—Е–∞ –њ–Њ–≥–ї—Г–±–ґ–µ) —Б–µ–Ї—В–Њ—А –≤ 2/3 –Њ–Ї—В–∞–≤—Л!!!
–≠—В–Њ –љ–Є–Ї—Г–і–∞ –љ–µ –≥–Њ–і–Є—В—Б—П.–≠—В–Њ –љ–µ –Є–Љ–µ–µ—В –њ–Њ–і —Б–Њ–±–Њ–є –љ–Є–Ї–∞–Ї–Њ–≥–Њ —Б–Љ—Л—Б–ї–∞.
–Я–Њ–ї—П—А–љ—Л–є –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А —Б–њ–µ–Ї—В—А–∞ –і–Њ–ї–ґ–µ–љ –њ–Њ–Ї–∞–Ј—Л–≤–∞—В—М —В—Г –ґ–µ –Ї–∞—А—В–Є–љ—Г, —З—В–Њ –Є SPAN, —В–Њ–ї—М–Ї–Њ –Њ–љ–∞ –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –Ї–∞–Ї –±—Л –Њ–±—С—А–љ—Г—В–∞ –≤–Њ–Ї—А—Г–≥ —В–Њ—З–Ї–Є. –Ґ–µ –ґ–µ –ї–µ–њ–µ—Б—В–Ї–Є —Б —В–Њ–є –ґ–µ —И–Є—А–Є–љ–Њ–є. –Ґ–µ –ґ–µ –њ—А–Њ–њ–Њ—А—Ж–Є–Є —И–Є—А–Є–љ—Л –ї–µ–њ–µ—Б—В–Ї–Њ–≤ –Є –њ—А–Њ–Љ–µ–ґ—Г—В–Ї–Њ–≤ –Љ–µ–ґ–і—Г –љ–Є–Љ–Є.
–•–Њ—В—П —Н—В–Њ –Є —Г–ґ–∞—Б–љ–Њ —Б–∞–Љ–Њ –њ–Њ —Б–µ–±–µ, –љ–Њ —П –±—Л –і–∞–ґ–µ —Б–Њ–≥–ї–∞—Б–Є–ї—Б—П, –µ—Б–ї–Є –±—Л –Њ–і–Є–љ–Њ—З–љ—Г—О –љ–Њ—В—Г ¬Ђ–Ф–Њ¬ї –Њ–љ –≤–Є–Ј—Г–∞–ї–Є–Ј–Є—А–Њ–≤–∞–ї –љ–µ –Ї–∞–Ї –Є–Ј—П—Й–љ—Л–є –ї–µ–њ–µ—Б—В–Њ–Ї, –∞ –Ї–∞–Ї –Њ–≥—А–Њ–Љ–љ—Л–є —Г–≥–ї–Њ–≤—Л–є 30¬∞-–љ—Л–є —Б–µ–Ї—В–Њ—А. –І—С—А—В —Б –љ–Є–Љ, –љ–Њ 120¬∞ –љ–∞ –Њ–і–љ—Г –љ–Њ—В—Г вАФ —Н—В–Њ –њ—А–Њ—Б—В–Њ –і–∞–ґ–µ —Б–ї–Њ–≤–∞–Љ–Є –љ–µ –≤—Л—А–∞–Ј–Є—В—М, –љ–∞—Б–Ї–Њ–ї—М–Ї–Њ –љ–µ–њ—А–Є–µ–Љ–ї–µ–Љ–Њ.
–Т –Њ–±—Й–µ–Љ, –Љ–Њ—П –Є–і–µ—П, –Ї–Њ—В–Њ—А–∞—П –Љ–љ–µ –њ—А–Є—И–ї–∞ —Г –≥–Њ–ї–Њ–≤—Г —Г–ґ–µ –Њ—З–µ–љ—М –і–∞–≤–љ–Њ, –Њ–љ–∞ –њ–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–ї–∞ —Б–Њ–Ј–і–∞–љ–Є–µ –∞–љ–∞–ї–Є–Ј–∞—В–Њ—А–∞, –Ї–Њ—В–Њ—А—Л–Љ –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П, –Ї–Њ—В–Њ—А—Л–є –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—О –≤ —В–Њ–Љ —Г–љ–Є–Ї–∞–ї—М–љ–Њ–Љ –≤–Є–і–µ, –≤ –Ї–Њ—В–Њ—А–Њ–Љ —З–µ–ї–Њ–≤–µ–Ї –µ—С –ї–µ–≥–Ї–Њ –Љ–Њ–ґ–µ—В –Є–љ—В–µ—А–њ—А–µ—В–Є—А–Њ–≤–∞—В—М, –≤ –Њ—В–ї–Є—З–Є–µ –Њ—В —В–µ—Е –≤–Є–і–Њ–≤, –≤ –Ї–Њ—В–Њ—А—Л—Е —Н—В–Њ –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—В –і—А—Г–≥–Є–µ —Б–њ–µ–Ї—В—А–Њ–∞–љ–∞–ї–Є–Ј–∞—В–Њ—А—Л –Є —Б–њ–µ–Ї—В—А–Њ-–≤—М—О–≤–µ—А—Л. –ѓ –і–Њ–ї–≥–Њ –Є—Б–Ї–∞–ї —Е–Њ—В—П –±—Л –Њ–і–љ—Г —А–µ–∞–ї–Є–Ј–∞—Ж–Є—О, –љ–Њ –љ–µ –љ–∞—И—С–ї –љ–Є –Њ–і–љ–Њ–є.
–Ъ —Б–Њ–ґ–∞–ї–µ–љ–Є—О, —В–µ–њ–µ—А—М –њ–Њ—Е–Њ–ґ–µ ¬Ђ–њ–µ—А–≤–∞—П –≤ –Є—Б—В–Њ—А–Є–Є¬ї —Г—В–Є–ї–Є—В–∞ –і–ї—П –њ–Њ–ї—П—А–љ–Њ–≥–Њ –≤—Л–≤–Њ–і–∞ —Б–њ–µ–Ї—В—А–∞ —Б–Њ–Ј–і–∞–љ–∞, –Є –≤—А–Њ–і–µ –±—Л –Ї–∞–Ї —Б–Њ–Ј–і–∞–љ–∞ –њ–Њ –Љ–Њ–µ–є –Є–і–µ–µ, –љ–Њ –і–Њ —В–Њ–≥–Њ, –Ї–∞–Ї –Њ–љ–∞ –і–Њ–ї–ґ–љ–∞ –њ–Њ –Љ–Њ–µ–є –Ј–∞–і—Г–Љ–Ї–µ (—Б –Њ—Б–љ–Њ–≤–љ–Њ–є –љ–∞ —А–∞—Б—Б–Ї–∞–Ј–∞–ї –Њ –Ї–Њ—В–Њ—А–Њ–є —Н—В–Њ –њ—А–Њ–≥—А–∞–Љ–Љ–Ї–∞ –Є –±—Л–ї–∞ —Б–Њ–Ј–і–∞–љ–∞), –µ–є –Ї–∞–Ї –і–Њ –Ъ–Є—В–∞—П –њ–µ—И–Ї–Њ–Љ, –Є —Н—В–Њ –Њ–±–Є–і–љ–Њ.
–Р–љ–∞–ї–Є–Ј–∞—В–Њ—А –њ–Њ–ї—Г—З–Є–ї—Б—П –љ–µ—О–Ј–∞–±–µ–ї—М–љ—Л–Љ –≤ –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Њ–Љ –њ–ї–∞–љ–µ: –љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ-–љ–Є–±—Г–і—М –±–Њ–ї–µ–µ —Б–µ—А—М—С–Ј–љ–Њ–Љ –Ј–∞–њ–Њ–ї–љ–µ–љ–љ–Њ–Љ —Б–њ–µ–Ї—В—А–µ –Њ–љ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –њ—А–Њ—Б—В–Њ –Ї–∞—И—Г –Є —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –Љ–Є–≥–∞—О—Й–Є–µ —Б–µ–Ї—В–Њ—А–∞ —Б –љ–µ–Њ–ґ–Є–і–∞–µ–Љ—Л–Љ–Є –≥—А–∞–љ–Є—Ж–∞–Љ–Є. –Ъ–∞–Ї —А–∞–Ј–≤–ї–µ–Ї–∞—В–µ–ї—М–љ–∞—П –±–µ–Ј–і–µ–ї—Г—И–Ї–∞ —Н—В–Њ –њ–Њ–є–і—С—В, –љ–Њ —Б–њ–µ–Ї—В—А–Њ–∞–љ–∞–ї–Є–Ј–∞—В–Њ—А –њ–Њ–Ї–∞ –љ–µ —Г–і–∞–ї—Б—П, —В–µ–Љ –±–Њ–ї–µ–µ —В–Њ—В, –Є–і–µ–µ–є –Ї–Њ—В–Њ—А–Њ–≥–Њ —П –њ–Њ–і–µ–ї–Є–ї—Б—П вАФ –њ–Њ–Ї–∞ –љ–µ –≤—Л—И–µ–ї.

















 .
. 











 .
.